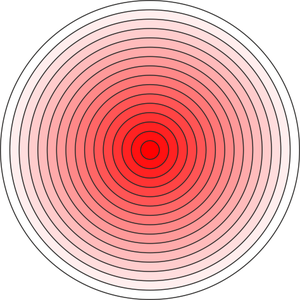
Masa de esfera no homogénea

De Laplace

1 Enunciado

La densidad de masa de una esfera de radio R viene dada por la ley

Sabiendo que el área de una superficie esférica de radio r vale 4πr², calcule el volumen y la masa de la esfera de radio R. ¿Cuánto vale su densidad media?

2 Volumen

La idea es calcular el volumen a partir de la suma de elementos de volumen de tamaño infinitesimal

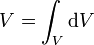
Entre los posibles elementos podemos considerar la esfera como compuesta de capas concéntricas , como las de una cebolla. Cada una de estas capas, de radio r comprendido entre 0 y R,es una lámina de área 4πr² y espesor dr, por lo que tiene un volumen diferencial

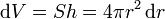
con lo que el volumen total será el conocido

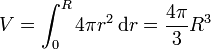
3 Masa

De manera análoga se calcula la masa de la esfera

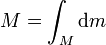
Por ser la densidad uniforme para cada valor de r, la masa de cada una de las capas anteriores será igual a la densidad de masa multiplicada por el volumen

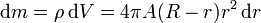
Dado que la densidad varía al aumentar el radio r, el centro de la esfera es la parte más densa Llevando esto a la integral

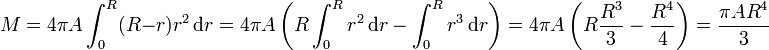
Una comprobación que siempre conviene hacer es verificar que las dimensiones son correctas y que a la hora de descomponer en dos integrales, no nos hemos olvidado ninguna potencia de R.

4 Densidad media

Una vez que tenemos el volumen y la masa total, la densidad media de masa es inmediata

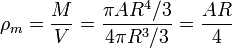
Obsérvese que ni el volumen, ni la masa, ni la densidad media son funciones de r sino solo de las constantes del problema, ya que no son funciones de la posición, sino que tienen un valor fijado para la esfera como un todo.