Dos rodillos con deslizamiento
De Laplace
Contenido |
1 Enunciado
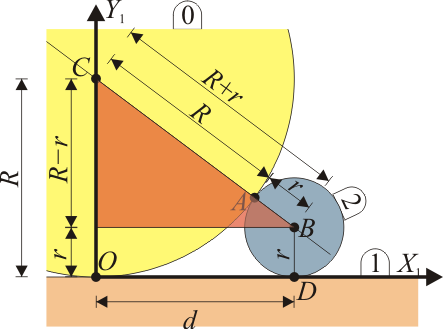
Un rodillo de radio 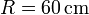 (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante
(sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante 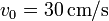 respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio
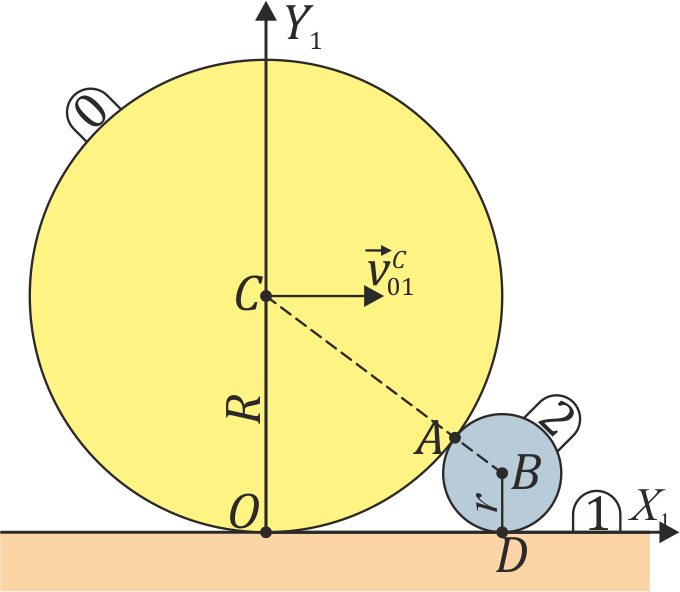
respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio 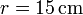 (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
(sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
- Calcule las velocidades angulares
 ,
,  y
y  .
.
- Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos
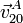 . ¿Cuál es la rapidez de este deslizamiento?
. ¿Cuál es la rapidez de este deslizamiento?
- Determine la posición del centro instantáneo de rotación I20 por los procedimientos siguientes: (i) analíticamente (con ayuda del resultado del apartado anterior); (ii) gráficamente.
2 Solución
2.1 Velocidades angulares
2.1.1 Movimiento {01}
El movimiento {01} es uno de rodadura sin deslizamiento alrededor del punto O de contacto del rodillo 0 con el suelo 1. La velocidad del punto C en este movimiento es igual a
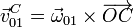
donde
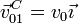
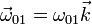
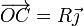
Sustituyendo en la expresión anterior

de donde
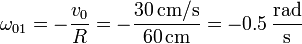
2.1.2 Movimiento {21}
Al ser empujado por el rodillo 0, el centro del rodillo 2 se ve forzado a avanzar con la misma rapidez, de forma que
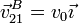
Al rodar sin deslizar sobre la superficie horizontal, el rodillo 2 efectúa un movimiento {21} de rotación en torno al punto D de contacto del rodillo con el suelo. Operando del mismo modo que en el caso anterior obtenemos
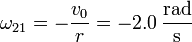
2.1.3 Movimiento {20}
La velocidad angular con la que un rodillo gira respecto al otro la obtenemos aplicando la ley de composición de las velocidades angulares
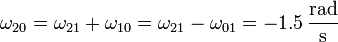
2.2 Velocidad de deslizamiento
El contacto entre los dos rodillos no es solo de rodadura, sino también de deslizamiento. En el punto en que son tangentes, el punto A del rodillo 0 se está moviendo hacia abajo, mientras que el punto A del rodillo 2 lo hace hacia arriba, con lo que existe una cierta velocidad relativa. El valor de esta velocidad es
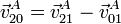
La velocidad del punto A en el movimiento {21} es igual a
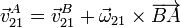
El vector de posición relativo cumple la relación de proporcionalidad
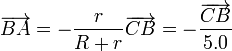
siendo el vector de posición relativo entre los ejes de la forma

La distancia d entre los puntos de contacto la obtenemos por aplicación del teorema de Pitágoras


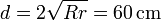
lo que nos da
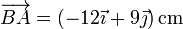
y la velocidad

Esta velocidad puede también hallarse reduciendo en el punto D, que es el CIR I21
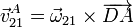
donde
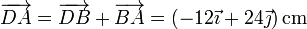
La velocidad en el movimiento {01} se calcula de manera similar. Reduciendo en el centro del rodillo 0
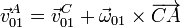
siendo ahora el vector de posición relativo
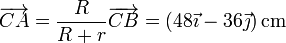
lo que resulta en la velocidad

Esta velocidad también puede calcularse como
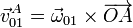
La velocidad de deslizamiento es la diferencia entre estas dos velocidades
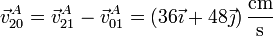
Esta velocidad relativa es tangente a la superficie de contacto y tiene por módulo
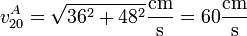
El que resulte el doble de la velocidad de avance de los rodillos no es casual ni dependiente de las dimensiones concretas de estos. Podemos demostrarlo de forma sencilla:
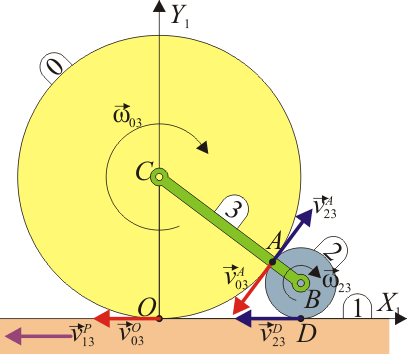
Observemos que los centros C y B se encuentran en todo momento a la misma distancia entre ellos, R + r. Por tanto, podemos imaginarnos un cuarto sólido, “3”, formado por una barra que une los dos centros. ¿Cómo son los diferentes movimientos respecto a esta barra?
- El sólido “1” el suelo se mueve hacia atrás con rapidez v0.
- El disco “0” gira alrededor de su centro C con una velocidad angular tal que el punto O se mueve hacia atrás con celeridad v0.
- El disco “2” gira alrededor de su centro B con una velocidad angular tal que el punto D se mueve hacia atrás con celeridad v0.
La velocidad de deslizamiento en A será la diferencia
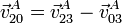
Ahora bien, en estos dos movimientos de rotación las velocidades de A son tangentes a la línea de contacto entre discos, las dos tienen módulo v0 y poseen sentidos opuestos. Por tanto, su diferencia será un vector también tangente y de módulo v0 − ( − v0) = 2v0. Este resultado es independiente de los radios de los discos.
2.3 Centro instantáneo de rotación
2.3.1 Método analítico
La posición del CIR I20 puede obtenerse analíticamente conocida la velocidad de un punto y la velocidad angular. La posición del CIR respecto al punto A es
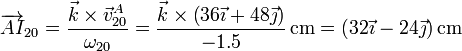
y respecto al punto O
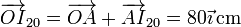
2.3.2 Métodos geométricos
Geométricamente, podemos determinar la posición del CIR {20} de diferentes formas.
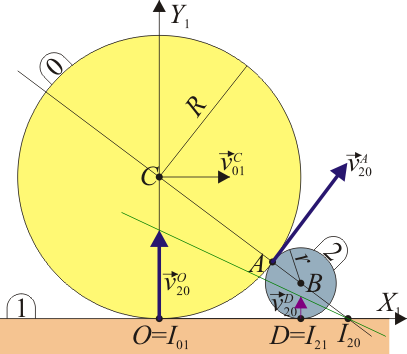
Una posibilidad consiste en hallar en primer lugar la velocidad de un segundo punto, en adición del que ya conocemos. Si consideramos la velocidad del punto O en el movimiento {20} obtenemos
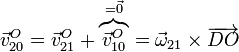
La velocidad de arrastre se anula por ser O el CIR del movimiento {10}. La segunda expresión nos dice que la velocidad de O en el movimiento {20} es perpendicular a la recta que pasa por D y O.
El CIR I20 se encuentra entonces en la intersección de la recta horizontal, que pasa por D y O, con la recta que une los centros C y B (perpendicular a la velocidad de deslizamiento en A).
Alternativamente, podemos observar que la distancia entre B y C permanece constante en todo momento, por lo que podemos imaginar un cuarto sólido 3, que une estos dos centros (una barra, por ejemplo). Los movimientos de los dos rodillos respecto al sólido 3 son rotaciones alrededor de los respectivos ejes B y C.
Aplicando ahora el teorema de los tres centros tenemos que el CIR I20 debe estar en la intersección de la recta que pasa por I01(O) e I21 (D), con la recta que pasa por I03 (C) e I23 (B), llegándose al resultado ya conocido.
Otra forma consiste en, si no se ha calculado la velocidad de deslizamiento en A, buscar otro punto cuya velocidad {20} sea fácil de calcular. El más simple es D, para el que tenemos
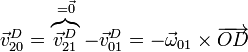
Sustituyendo los valores numéricos queda
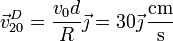
Que junto con el resultado anterior
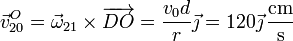
permite aplicar el método geométrico de determinación del CIR para el caso de que tengamos dos velocidades paralelas.
También puede hallarse gráficamente con ayuda del sólido “3” introducido en el apartado anterior. Según hemos dicho, por el teorema de los tres centros, el CIR I20 debe estar en la intersección de la recta que pasa por I01(O) e I21 (D). Además debe estar sobre la recta que pasa por el CIR I03 (que es el centro del rodillo “0”, C) y con el CIR I23 (que es el centro B del rodillo “2”). De nuevo llegamos a que debe estar en la intersección de la recta que pasa por O y D con la que pasa por B y C.