Conexiones de dos bombillas

De Laplace

1 Enunciado

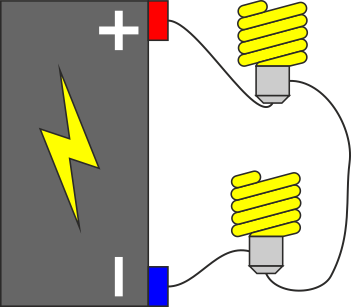
Se desea encender dos bombillas de resistencia R₀, para lo cual se dispone de una batería de f.e.m. 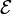y resistencia interna r.

1. En un primer montaje se disponen las dos bombillas en serie.
   1. Calcule la intensidad de corriente que circula por cada una.
   2. Halle la potencia que consumen (que dará una medida de la luz que desprenden).
   3. Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
2. A continuación se prueba a montarlas en paralelo.
   1. Calcule la intensidad de corriente que circula por cada una.
   2. Halle la potencia que consumen.
   3. Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
3. ¿En cuál de los dos montajes el conjunto de las dos bombillas dará más luz?
4. Supongamos que tenemos una batería de 10 V y 1 Ω de resistencia interna y dos bombillas en cuya etiqueta pone “10V 25W”, ¿cómo deberemos montarlas para que den el máximo de luz? ¿Cuánta potencia consumirán en ese caso?

        

2 Bombillas en serie

Si las dos bombillas están en serie, el modelo del sistema es un circuito sencillo formado por cuatro elementos en serie:

• Una fuente ideal de f.e.m
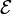
• La resistencia interna de la fuente, r
• Las dos resistencias de las dos bombillas.

En este circuito la corriente que circula por él es igual a la f.e.m. dividida por la suma de todas las resistencias

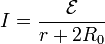
La potencia disipada en las dos bombillas conjuntamente es

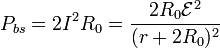
La potencia generada por la fuente vale

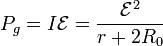
y la consumida en la propia fuente es la diferencia entre las dos anteriores

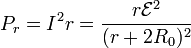
3 Bombillas en paralelo

Si las dos bombillas están en paralelo, la diferencia de potencial entre sus extremos es la misma para los dos e igual a la tensión a la salida de la fuente

siendo I₁ la corriente que circula por una bombilla (que al ser las dos iguales, será idéntica a la que pasa por la otra).

La tensión a la salida de la fuente no es igual a la f.e.m., por no ser la fuente ideal, sino que hay una caída de tensión en la resistencia interna

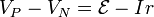
siendo

Nos queda entonces que la corriente que va por cada bombilla es

y la potencia consumida en las dos bombillas es

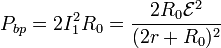
La potencia inyectada por la fuente en el sistema es, en este caso,

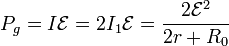
y la consumida en la propia fuente

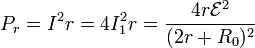
cumpliéndose como antes que

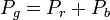
4 Comparación de los dos sistemas

Para ver en cuál de las dos configuraciones se produce mayor cantidad de luz, comparamos las potencias consumidas por las bombillas en cada caso y queda la proporción

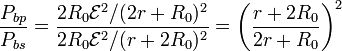
que también se puede escribir como

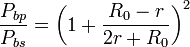
El resultado depende por tanto de la proporción entre la resistencia de las bombillas y la interna de la fuente:

• Si la resistencia de cada bombilla es superior a la interna el numerador es mayor que el denominador y las bombillas en paralelo dan más luz que en serie.
• Si R₀ < r la configuración en serie es la más luminosa.

Si las dos resistencias son iguales, las configuraciones son equivalentes.

En un caso real siempre es preferible montarlas en paralelo ya que la resistencia de una bombilla puede rondar los kiloohmios, mientras que la interna de una fuente puede ser del orden de 1 Ω.

5 Caso práctico