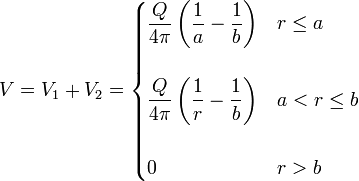Entrar Página Discusión Historial Go to the site toolbox

Energía electrostática de superficies esféricas

De Laplace

Contenido

1 Enunciado

Calcule la energía electrostática almacenada en las siguientes distribuciones de carga:

  1. Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga Q.
  2. Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas uniformemente cargas + Q y − Q respectivamente.
  3. Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas cargas con densidades + σ0 y − σ0 respectivamente.

2 Introducción

La energía electrostática de una densidad de carga superficial es una generalización de la energía d eun sistema de cargas puntuales

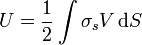
U = \frac{1}{2}\int \sigma_s V\,\mathrm{d}S

donde σs es la densidad superficial de carga y V es el potencial eléctrico en los puntos donde se encuentra esta. Este potencial eléctrico es debido a todas las fuentes de campo eléctrico que haya, no solo el debido a la propia densidad superficial.

3 Una superficie esférica

Una superficie esférica cargada uniformemente produce el potencial eléctrico

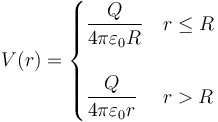
V(r)=\begin{cases} \displaystyle \frac{Q}{4\pi\varepsilon_0R} & r \leq R \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r > R \end{cases}

Para hallar la energía debemos calcular la integral

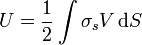
U = \frac{1}{2}\int \sigma_s V\,\mathrm{d}S

sobre los puntos de la superficie esférica. En estos puntos el potencial vale

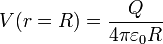
V(r=R)=\frac{Q}{4\pi\varepsilon_0R}

Vemos que tiene el mismo valor en todos los puntos de la superficie esférica. Esto nos da la energía

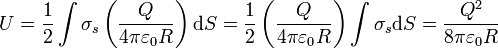
U = \frac{1}{2}\int\sigma_s\left(\frac{Q}{4\pi\varepsilon_0R}\right)\mathrm{d}S=\frac{1}{2}\left(\frac{Q}{4\pi\varepsilon_0R}\right)\int \sigma_s\mathrm{d}S=\frac{Q^2}{8\pi\varepsilon_0R}

donde hemos aplicado que la integral de la densidad de carga es la carga total

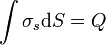
\int \sigma_s\mathrm{d}S=Q

A la vista del resultado podemos extraer una serie de conclusiones:

  • La energía electrostática es independiente del signo de la carga. Una esfera cargada negativamente tiene una energía positiva.
  • La energía electrostática es siempre positiva (o nula en el caso de una esfera descargada).
  • La energía es cuadrática con la carga. Esto quiere decir que si una esfera de 1cm almacena una carga de 1nC, la energía electrsática es de 0.9μJ, pero si queremos almacenar 1μC (1000 veces más carga) necesitamos multiplicar la energía no por 1000 veces sino por 1.000.000 veces.
  • La energía es inversamente proporcional al radio de la esfera y no es proporcional a su volumen. Esto quiere decir que si aumentamos el radio al doble la energía no se multiplica por 8, sino que por el contrario se reduce a la mitad.

4 Dos superficies con cargas opuestas

En el caso de las dos esferas concéntricas no es la suma de las energías de las dos esferas por separado. La energía electrostática no cumple el principio de superposición.

Para hallar la energía, calculamos el potencial total producido por las dos esferas simultáneamente. El debido a la esfera interior (que etiquetaremos como “1”) es

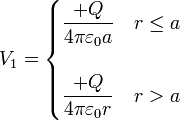
V_1=\begin{cases} \displaystyle \frac{+Q}{4\pi\varepsilon_0a} & r \leq a \\ & \\ \displaystyle\frac{+Q}{4\pi\varepsilon_0 r} & r > a \end{cases}

y el debido a la exterior (“2”) es

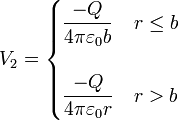
V_2=\begin{cases} \displaystyle \frac{-Q}{4\pi\varepsilon_0b} & r \leq b \\ & \\ \displaystyle\frac{-Q}{4\pi\varepsilon_0 r} & r > b \end{cases}

El potencial total es la suma de estos dos

V = V_1 + V_2 = \begin{cases} \displaystyle \frac{Q}{4\pi}\left(\frac{1}{a}-\frac{1}{b}\right) & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi}\left(\frac{1}{r}-\frac{1}{b}\right) & a < r \leq b \\ & \\ 0 & r > b \end{cases}

5 Dos superficies con densidades opuestas

Obtenido de "http://tesla.us.es/wiki/index.php/Energ%C3%ADa_electrost%C3%A1tica_de_superficies_esf%C3%A9ricas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace