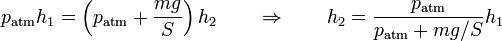Compresión isoterma de un gas
De Laplace
1 Enunciado
Un cilindro vertical de 10.0 cm de diámetro contiene hidrógeno a 25°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Se coloca sobre la tapa una pesa de 2.0 kg. Halle la altura de la tapa una vez que se alcanza de nuevo el equilibrio térmico con el exterior. ¿A qué temperatura habrá que calentar el gas para que la tapa vuelva a su posición inicial, con el peso todavía encima?
2 Compresión isoterma
Cuando se coloca la pesa sobre el émbolo, aumenta la presión sobre el gas, siendo la nueva presión ejercida

Al ser esta presión superior a la interior, aparece una fuerza sobre el pistón y este desciende. Al hacerlo comprime el gas, aumentando su presión. En un proceso real, la presión interior llega a superar a la exterior, causando una fuerza hacia arriba y un “rebote” del émbolo. Tras una serie de oscilaciones, el pistón se detiene en una posición de equilibrio, en la que la presión del gas iguala a la exterior. Puesto que en el estado final la temperatura final iguala a la inicial, podemos aplicar la ley de Boyle
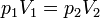
siendo
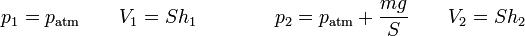
lo que nos da