Prisma entre placas conductoras

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Matriz de coeficientes de capacidad 2.2 Cargas y potenciales en las placas. Energía en el sistema 2.3 Presión electrostática y fuerza neta sobre el prisma

1 Enunciado

Se tiene el sistema de la figura, formado por un prisma triangular (“4”), cuya base es un triángulo equilátero de lado L, y cuya altura es también L. Este prisma está conectado a tierra. Frente a él se encuentran tres placas cuadradas de lado L situadas a distancia a, 2a y 3a (), respectivamente. Las placas “1” y “3” se conectan a un voltaje V₀, mientras que la “2” almacena una carga Q₀

1. Halle la matriz de coeficientes de capacidad en este sistema de cuatro conductores. Desprecie los efectos de borde.
2. Calcule la carga y el potencial de cada placa, así como la energía total del sistema.
3. Calcule la presión electrostática en cada cara del prisma. A partir de la presión, halle la fuerza neta sobre el prisma.

2 Solución

2.1 Matriz de coeficientes de capacidad

Para calcular los coeficientes de capacidad del sistema bajo estudio, obtendremos primero los elementos de su circuito equivalente. Éste es, sin duda, el procedimiento más simple.

El conductor ``4" está conectado a tierra, por tanto, los consideraremos como conductor de referencia. Y como los efectos de borde son despreciables, pues 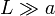, podemos asumir que cada uno de los conductores ``1", ``2" y ``3" se encuentran en influencia total con el ``4". O lo que es lo mismo, este conductor actúa de pantalla entre los otros. Por tanto, se tendrá que...

2.2 Cargas y potenciales en las placas. Energía en el sistema

2.3 Presión electrostática y fuerza neta sobre el prisma