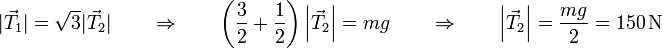Partícula suspendida de dos hilos
De Laplace
Revisión a fecha de 09:04 21 ene 2012; Antonio (Discusión | contribuciones)
1 Enunciado
Una partícula de peso 300 N cuelga de un techo horizontal sujeta por dos hilos (“1” y “2”). El hilo 1 forma un ángulo de 30° con la vertical, mientras que el hilo 2 forma uno de 60° con la vertical. ¿Cuánto valen, en módulo, las tensiones de los dos hilos?
2 Solución
Puesto que la masa está en equilibrio, la suma de las fuerzas que actúan sobre ella es nula
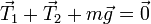
proyectando sobre un sistema de ejes en el que el eje OX es el horizontal en el plano de los dos hilos y el eje Z es el vertical expresamos estas fuerzas como
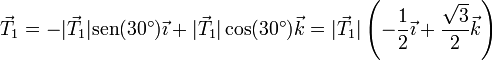
y
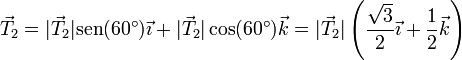
siendo el peso
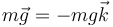
Puesto que la suma vectorial de las fuerzas se anula

Despejando de la primera y sustituyendo en la segunda