Problemas de Movimiento oscilatorio (GIC)

De Laplace

Revisión a fecha de 11:47 10 ene 2012; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Pelota que bota y bota

Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple?

2 Solución general del MAS

La solución general de la ecuación de movimiento

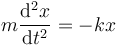
$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -k x$

es de la forma

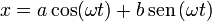
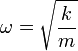
$x = a \cos(\omega t)+b\,\mathrm{sen}\,(\omega t)$ $\omega=\sqrt{\frac{k}{m}}$

con $a$ y $b$ dos constantes dependientes de las condiciones iniciales.

Halle el valor de las constantes $a$ y $b$ si la posición inicial de la partícula es $x 0$ y su velocidad inicial es $v 0$ .
Demuestre que la ecuación horaria 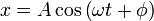$x = A \cos\left(\omega t+\phi\right)$ es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes ${A,φ}$ y las constantes ${a, b}$ . Exprese $A$ y $φ$ en función de la posición y la velocidad iniciales, $x 0$ y $v 0$ .
Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
Demuestre que la cantidad $E = m v 2 / 2 + k x 2 / 2$ no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
Demuestre que $x = e jω t$ , con 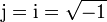$\mathrm{j}=\mathrm{i}=\sqrt{-1}$ , la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación