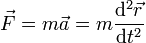Fuerza en anilla ensartada en varillas
De Laplace
Revisión a fecha de 10:50 26 nov 2011; Antonio (Discusión | contribuciones)
1 Enunciado
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ´esta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.
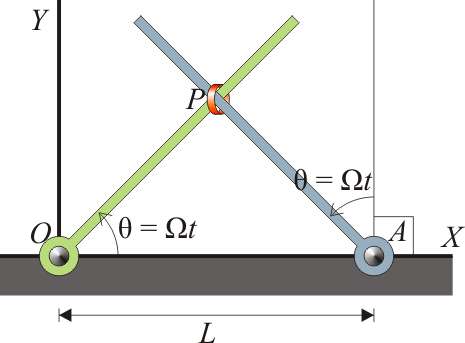
2 Sin considerar el peso
Conocemos el movimiento de la anilla: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular 2Ω y el radio de giro L / 2. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda,
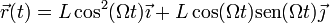
La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton