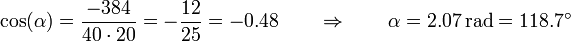Cálculo de ángulo entre dos vectores

De Laplace

Revisión a fecha de 16:55 13 nov 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Halle el ángulo que forman los vectores

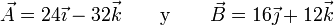
$\vec{A}=24\vec{\imath}-32\vec{k}\qquad\mbox{y}\qquad \vec{B}=16\vec{\jmath}+12\vec{k}$

2 Solución

Obtenemos el ángulo a partir del producto escalar de los dos vectores

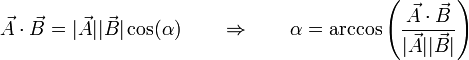
$\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos(\alpha)\qquad\Rightarrow\qquad \alpha = \arccos\left(\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|}\right)$

Tenemos que

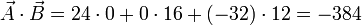
$\vec{A}\cdot\vec{B}=24\cdot 0+0\cdot 16+(-32)\cdot 12=-384$

y que

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): |\vec{A}| = \sqrt{\vec{A}\cdot\vec{A}}=\sqrt{24^2^2+0^2+(-32)^2} = 40\qquad |\vec{B}| = \sqrt{\vec{B}\cdot\vec{B}}=\sqrt{0^2+16^2+12^2} = 20

lo que nos da

$\cos(\alpha)=\frac{-384}{40\cdot20}=-\frac{12}{25}=-0.48\qquad\Rightarrow\qquad \alpha = 2.07\,\mathrm{rad}=118.7^\circ$

Cálculo de ángulo entre dos vectores

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES