Ejemplo de operaciones con dos vectores
De Laplace
Revisión a fecha de 14:58 8 oct 2011; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Dados los vectores

- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
 como suma de dos vectores, uno paralelo a
como suma de dos vectores, uno paralelo a  y otro ortogonal a él.
y otro ortogonal a él.
2 Ángulo
Obtenemos el ángulo a partir del producto escalar de los dos vectores
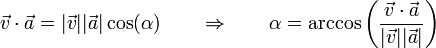
Tenemos que
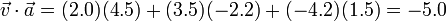
y que
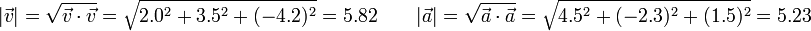
lo que nos da