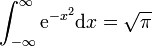Pulso gaussiano de tensión
De Laplace
Revisión a fecha de 17:40 28 feb 2011; Antonio (Discusión | contribuciones)
Enunciado
Se tiene un condensador con pérdidas formado por dos placas cuadradas de lado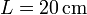 
, situadas paralelamente a una distancia 
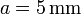. Entre ellas se encuentra un material de permitividad relativa 
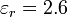y conductividad 
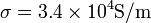. Una placa se encuentra permanentemente a tierra, mientras que la otra experimenta un pulso de tensión de forma gaussiana
con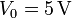 
y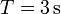 
.
Para cualquier instante de tiempo, calcule
- la distribución de campo eléctrico y de corriente entre las placas. Desprecie los efectos de borde.
- la carga en cada una de las placas y la corriente que llega a cada una.
- la energía electrostática almacenada, la potencia disipada en el medio, y la potencia desarrollada por el generador.
- Calcule igualmente la energía total disipada a lo largo del tiempo, así como el trabajo total realizado por el generador.
Halle el valor numérico de los resultado sélo para el último apartado.
Dato:
