5.7. Movimiento relativo de dos ventiladores
De Laplace
Contenido |
1 Enunciado
Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos “0” y “2”) de orientación fija, ambos a la misma altura, y con sus respectivos centros (A y B) equidistantes (distancia L) de la esquina (punto O). Los dos ventiladores rotan con velocidad angular de módulo constante igual a ω, si bien lo hacen con las orientaciones y sentidos respectivamente indicados en la figura. Definido el triedro fijo OXYZ (sólido “1”) del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determine
-
 y
y 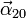
-
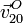 y
y 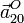 ;
;
- El eje instantáneo de rotación (E.I.R.) del movimiento {20}.
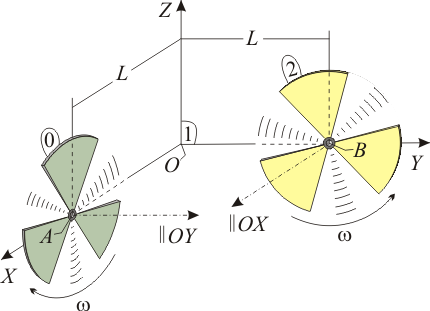
Nota: Se recomienda la utilización del triedro “1” para la descomposición del movimiento-problema, así como el uso de su base vectorial para resolver el ejercicio.
2 Velocidad y aceleración angular
2.1 Velocidad angular
En este caso tenemos la descomposición
La velocidad angular es la suma de las de los dos movimientos relativos
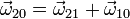
La velocidad angular del movimiento {21} va en la dirección del eje OX
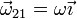
La del movimiento {10} es igual en magnitud, y de sentido opuesto a la del movimiento {01}, que es el dato que se nos da
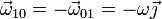
por lo que la velocidad angular absoluta vale