Velocidad de escape
De Laplace
Solución
La velocidad de escape se define como la mínima velocidad que es preciso comunicar a un cuerpo ligero para salir del campo gravitatorio de otro masivo.
Esta velocidad mínima es la que permite llegar al infinito con velocidad nula. Una velocidad menor no permitiría salir del “pozo” de energía potencial gravitatoria.
La energía mecánica de una partícula en un campo gravitatorio es
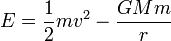
Imponiendo que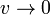 
cuando 
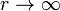queda
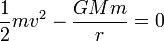
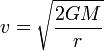
Aquí r es la distancia de partida. En el caso de un cohete que parte de la superficie terrestre r = RT. El valor de GM lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre
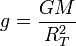
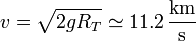
Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol.
