Despolarización de una esfera
De Laplace
1 Enunciado
Una esfera de radio a se despolariza según la ley
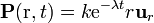
Determine las densidades de carga de polarización, así como la densidad de corriente de polarización. ¿Se verifica la ley de conservación de la carga para ρp y σp?
2 Solución
Las densidades de carga de polarización pueden ser de volumen o de superficie. En el primer caso \[ \rho_p = -\nabla{\cdot}\mathbf{P} = -k\mathrm{e}^{-\lambda t}\nabla{\cdot}\br = -3k\mathrm{e}^{-\lambda t} \] en el interior de la esfera ($r<a$), mientras que en su exterior esta densidad es nula, ya que no hay polarización.
La carga de polarización almacenada en el volumen valdrá, por ser la densidad uniforme, \[ Q_v = \int \rho_p \,d\tau = \left(\frac{4\pi}{3}a^3\right)\left(-3k\mathrm{e}^{-\lambda t}\right)
= -4\pi a^3 k\mathrm{e}^{-\lambda t}
\]
Las densidades de carga superficiales se encontrarán en $r=a$ \[ \sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]= -\mathbf{u}_{r}{\cdot}\left(0-k\mathrm{e}^{-\lambda t}a\mathbf{u}_{r}\right)=k\mathrm{e}^{-\lambda t}a \] siendo la carga total almacenada en la superficie \[ Q_s =\int \sigma_p\,\mathrm{d}S =\left(4\pi a^2\right)\left(ka\mathrm{e}^{-\lambda t} \right)= 4\pi a^3 \mathrm{e}^{-\lambda t} \] Tanto la carga de volumen como la de superficie disminuyen en magnitud a lo largo del tiempo. La carga total de polarización será nula en todo instante \[ Q_p = Q_v + Q_s = 0 \] \indent La densidad de corriente de polarización valdrá en el interior de la esfera \[ \mathbf{J}_p = \frac{\partial{}\mathbf{P}}{\partial{}t} = -\lambda k \mathrm{e}^{-\lambda t} r\mathbf{u}_{r} \] y será nula en el exterior.
Esta densidad de corriente verifica la ley de conservación de la carga para $\rho_p$ y para $\sigma_p$. En el primer caso tenemos \[ \nabla{\cdot}\mathbf{J}_p = -3\lambda k\mathrm{e}^{-\lambda t} \qquad\frac{\partial{}\rho_p}{\partial{}t} = 3\lambda k \mathrm{e}^{-\lambda t} \] \[ \nabla{\cdot}\mathbf{J}_p+\frac{\partial{}\rho_p}{\partial{}t}=0 \] Para las superficiales empleamos la condición de salto \[ \mathbf{n}{\cdot}[\mathbf{J}_p]= \mathbf{u}_{r}{\cdot}\left(0+\lambda k \mathrm{e}^{-\lambda t}a\mathbf{u}_{r}\right) = \lambda k a \mathrm{e}^{-\lambda t} \]\[ \frac{\partial{}\sigma_s}{\partial{}t} = -\lambda k a \mathrm{e}^{-\lambda t}\qquad \mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial{}\sigma_s}{\partial{}t} \] Por supuesto, la ley de conservación de la carga puede demostrarse de forma general a partir de la definición de $\rho_p$, $\sigma_p$ y $\mathbf{J}_p$ \[ \rho_p = -\nabla{\cdot}\mathbf{P} \qquad \mathbf{J}_p = \frac{\partial{}\mathbf{P}}{\partial{}t} \] \[ \nabla{\cdot}\mathbf{J}_p = \nabla{\cdot}\left(\frac{\partial{}\mathbf{P}}{\partial{}t}\right) = \frac{\partial{}\ }{\partial{}t}\left(\nabla{\cdot}\mathbf{P}\right)= -\frac{\partial{}\rho_p}{\partial{}t} \] y análogamente para las densidades de superficie \[ \sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}] \] \[ \mathbf{n}{\cdot}[\mathbf{J}_p] = \mathbf{n}{\cdot}\left[\frac{\partial{}\mathbf{P}}{\partial{}t}\right] = \frac{\partial{}\ }{\partial{}t}\left(\mathbf{n}{\cdot}[\mathbf{P}]\right)= -\frac{\partial{}\sigma_p}{\partial{}t} \]





