1.4. Dependencias del periodo de un péndulo
De Laplace
1 Enunciado
Un péndulo simple es una masa m suspendida de un hilo ideal (sin masa), que tiene una longitud l. La masa está sometida a la aceleración de la gravedad, g.
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
2 Posibles dependencias
El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, l; la aceleración de la gravedad, g; la masa m; y la amplitud inicial con la que se separa de la vertical,θ0.
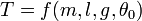
Sin embargo, esta función no es arbitraria, ya que la ecuación debe ser dimensionalmente correcta. Si el primer miembro tiene dimensiones de tiempo, el segundo debe tenerlo también.
¿Qué combinación de estos cuatro factores produce un tiempo? Tenemos que m tiene dimensiones de masa, l de longitud, g es una aceleración (LT²) y el ángulo inicial es adimensional. Para obtener un tiempo suponemos un producto de los diferentes factores
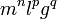
que tiene dimensiones





