1.12. Ejemplo de construcción de una base

De Laplace

Revisión a fecha de 17:15 21 jul 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Primer vector
3 Segundo vector
4 Tercer vector

1 Enunciado

Dados los vectores

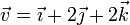
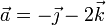
$\vec{v}=\vec{\imath}+2\vec{\jmath}+2\vec{k}$ $\vec{a}=-\vec{\jmath}-2\vec{k}$

Construya una base ortonormal dextrógira, tal que

El primer vector vaya en la dirección de $\vec{v}$
El segundo esté contenido en el plano definido por $\vec{v}$ y $\vec{a}$
El tercero sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.

2 Primer vector

Obtenemos el primer vector normalizando el vector $\vec{v}$ , esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo este vector por su módulo

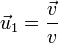
$\vec{u}_1=\frac{\vec{v}}{v}$

Hallamos el módulo de $\vec{v}$

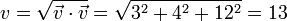
$v = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{3^2+4^2+12^2}=13$

por lo que

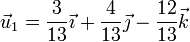
$\vec{u}_1 = \frac{3}{13}\vec{\imath}+\frac{4}{13}\vec{\jmath}-\frac{12}{13}\vec{k}$

3 Segundo vector

El segundo vector debe estar en el plano definido por $\vec{v}$ y $\vec{a}$ , por lo que debe ser una combinación lineal de ambos

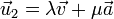
$\vec{u}_2 = \lambda\vec{v}+\mu\vec{a}$

además debe ser ortogonal a 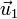$\vec{u}_1$ (y por tanto, a $\vec{v}$ )

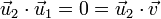
$\vec{u}_2\cdot\vec{u}_1 = 0 = \vec{u}_2\cdot\vec{v}$

y debe ser unitario

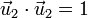
$\vec{u}_2\cdot\vec{u}_2=1$

El procedimiento sistemático consiste en hallar la componente de $\vec{a}$ normal a $\vec{v}$ y posteriormente normalizar el resultado.

La proyección normal la calculamos con ayuda del doble producto vectorial

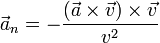
$\vec{a}_n = -\frac{(\vec{a}\times\vec{v})\times\vec{v}}{v^2}$

Calculamos el primer producto vectorial

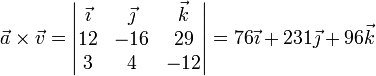
$\vec{a}\times\vec{v}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 12 & -16 & 29\\ 3 & 4 & -12\end{matrix}\right|=76\vec{\imath}+231\vec{\jmath}+96\vec{k}$

Hallamos el segundo

$\vec{a}\times\vec{v})\times \vec{v}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 56 & 231 & 96 \\ 3 & 4 & -12 \end{matrix}\right|=-76\vec{\imath}-231\vec{\jmath}-96\vec{k}$

4 Tercer vector

1.12. Ejemplo de construcción de una base

De Laplace

Contenido

1 Enunciado

2 Primer vector

3 Segundo vector

4 Tercer vector

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES