Campos en un condensador en CA
De Laplace
Contenido |
1 Enunciado
Se tiene un condensador formado por dos placas circulares planas y paralelas, de radio b y separadas una distancia a (
); entre ellas hay vacío. Entre los centros de las placas se establece una tensión V0cosωt.
- Halle, en primera aproximación, el campo eléctrico que se establece entre las placas.
- Determine el campo magnético inducido en el espacio entre las placas, según la ley de Ampère-Maxwell.
- Calcule, la primera corrección en el campo eléctrico obtenido en (1), de acuerdo con la ley de Faraday. ¿Para qué valor del radio empieza a ser importante esta corrección (esto es, comparable al campo estático)?
- Indique como serían las siguientes correcciones, tanto en
como en 
.
2 Solución
Éste es el típico problema que se plantea a la hora de estudiar las limitaciones de la teoría de circuitos. Por ello, suele aparecer en casi todos los libros de texto.
La idea es resolver las ecuaciones de Maxwell a base de correcciones sucesivas, en lugar de intentar resolverlas completamente de entrada, esto es, se trata de obtener un \emph{desarrollo perturbativo}. Veámoslo paso a paso.
2.1 Campo eléctrico
Si admitimos que ambas placas son perfectamente conductoras el campo eléctrico en el interior de las mismas es estrictamente nulo y, en primera aproximación, las superficies son equipotenciales. Si despreciamos los efectos de borde, el campo en todos los puntos entre las placas es el mismo e igual a
2.2 Campo magnético
Hemos supuesto que la fórmula anterior es válida cualquiera que sea el voltaje entre las placas, inclusive si es variable con el tiempo (como es el caso). Ahora bien, según la ley de Ampère--Maxwell, la circulación del campo magnético debe incluir la presencia de un campo eléctrico variable. Expresando esta ley en forma integral como
y aplicándola a un contorno circular centrado en el eje, resulta que el primer miembro, dada la simetría del sistema, es
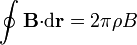
mientras que el segundo vale (teniendo en cuenta que la corriente de conducción es nula en el interior del condensador)
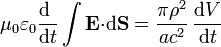
donde
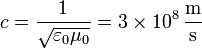
es la velocidad de la luz en el vacío.
Igualando estas dos expresiones llegamos al campo magnético en el interior del condensador
Vemos que el campo es acimutal y crece con la distancia al eje (ya que al alejarnos del mismo abarcamos una cantidad mayor de corriente de desplazamiento).
