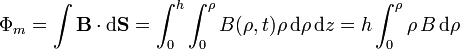Entrar Página Discusión Historial Go to the site toolbox

Campo eléctrico inducido por un cable grueso

De Laplace

Contenido

1 Enunciado

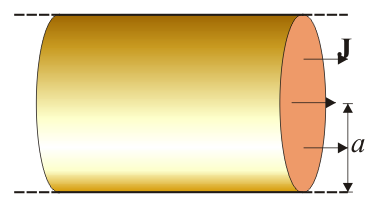
Por un hilo rectilíneo cilíndrico de radio a y gran longitud circula una corriente alterna de baja frecuencia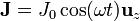 \mathbf{J}=J_0\cos(\omega t)\mathbf{u}_z.
  1. Halle el campo magnético producido por este hilo, tanto en su interior como en su exterior, suponiendo que la corriente es casi estacionaria.
  2. Halle el campo eléctrico inducido por este campo magnético tanto en el interior del cable como en su exterior, suponiendo que 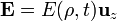\mathbf{E} = E(\rho,t)\mathbf{u}_z y que en el eje del cilindro el campo eléctrico es nulo.
  3. Calcule la densidad de corriente de desplazamiento en el interior y el exterior del hilo.

2 Campo magnético debido al cable

Al tratarse de una corriente casi estacionaria, el campo magnético puede calcularse como en el caso de un cable grueso recorrido por una corriente continua. Tal como se ve en el tema de campo magnético de corrientes estacionarias, el campo que produce este cable es

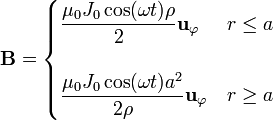
\mathbf{B}=\begin{cases}\displaystyle\frac{\mu_0J_0\cos(\omega t)\rho}{2}\mathbf{u}_\varphi & r\leq a\\ & \\ \displaystyle\frac{\mu_0J_0\cos(\omega t)a^2}{2\rho}\mathbf{u}_\varphi & r\geq a\end{cases}

3 Campo eléctrico inducido

Para hallar el campo eléctrico inducido por este campo magnético variable en el tiempo debemos usar la ley de Faraday. Podemos calcular el campo bien empleando la forma integral de la ley, bien su forma diferencial.

3.1 Forma integral

La ley de Faraday nos dice que, dada una curva cerrada fija, en un campo magnético variable en el tiempo, la fuerza electromotriz equivale a la derivada del flujo magnético cambiada de signo:

\mathcal{E}=\oint \mathbf{E}\cdot\mathrm{d}\mathbf{r} = -\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}=-\frac{\mathrm{d}\ }{\mathrm{d}t}\int\mathbf{B}\cdot\mathrm{d}\mathbf{S}

Puesto que se nos dice que el campo eléctrico inducido es longitudinal y dependiente sólo de la distancia al eje (y del tiempo), podemos aprovechar esto calculando la f.e.m. a lo largo de un contorno rectangular vertical, uno de cuyos lados coincide con el eje Z. Este rectángulo posee altura h a lo largo del eje, y anchura ρ. En este caso

\oint\mathbf{E}\cdot\mathbf{r} = \int_{0}^h\overbrace{E_z(\rho=0)}^{=0}\,\mathrm{d}z+\int_{0}^\rho \overbrace{E_\rho(z=h)}^{=0}\,\mathrm{d}\rho + \int_{h}^0E_z(\rho)\,\mathrm{d}z+\int_{\rho}^0 \overbrace{E_\rho(z=h)}^{=0}\,\mathrm{d}\rho = -E(\rho)h

Esta circulación debe ser igual a la derivada, cambiada de signo, del flujo del campo magnético a través de una superficie apoyada enla curva y orientada según la regla de la mano derecha.

Si tomamos como superficie el rectángulo delimitado por los segmentos anteriores, el vector normal es 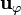\mathbf{u}_\varphi y el flujo correspondiente tiene la expresión

\Phi_m = \int \mathbf{B}\cdot\mathrm{d}\mathbf{S}= \int_0^h\int_0^\rho B(\rho,t)\rho\,\mathrm{d}\rho\,\mathrm{d}z = h\int_0^\rho\rho\,B\,\mathrm{d}\rho

3.2 Forma diferencial

4 Densidad de corriente de desplazamiento

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_el%C3%A9ctrico_inducido_por_un_cable_grueso"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace