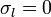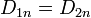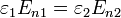Dieléctrico lineal

De Laplace

Revisión a fecha de 09:42 11 jun 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción. Relaciones constitutivas
2 Definición
- 2.1 Medio anisótropo
- 2.2 Medio isótropo
3 Modelo microscópico
4 Permitividad
- 4.1 Permitividad relativa
- 4.2 Permitividad absoluta
5 Efecto de un campo sobre un dieléctrico lineal
- 5.1 Partícula en un campo externo
- 5.2 Condensador lleno de dieléctrico
6 Conductores en presencia de medios lineales
- 6.1 Ejemplo. El condensador plano
7 Energía en un medio lineal
8 Presión en un dieléctrico
9 Dependencia temporal. Dispersión

1 Introducción. Relaciones constitutivas

Los medios dieléctricos se caracterizan por la presencia de dipolos, que contribuyen al campo eléctrico total. Estos dipolos se pueden modelar macroscópicamente mediante su densidad, la polarización 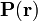$\mathbf{P}(\mathbf{r})$ .

Cuando la polarización es conocida, puede determinarse el campo eléctrico que produce, bien por integración directa, bien sustituyendo la polarización por densidades de carga equivalentes y aplicando las técnicas de cálculo de campos producidos por cargas eléctrica.

Sin embargo, en la mayoría de las situaciones la polarización no es conocida a priori, ya que la aparición de dipolos se debe usualmente a la propia presencia del campo eléctrico. Por tanto, la polarización es tanto causa como efecto del campo eléctrico. Para hallar $\mathbf{E}$ debemos conocer $\mathbf{P}$ y para conocer $\mathbf{P}$ debemos hallar $\mathbf{E}$ .

Podemos escapar de este círculo vicioso estableciendo empíricamente (o mediante un modelo acertado) una relación constritutiva

$\mathbf{P}=\mathbf{P}(\mathbf{E})\,$

que establezca cuánto vale la polarización para un cierto valor del campo total 8que incluye al de la propia polarización). Sustituyendo esta relación en las ecuaciones de la electrostática reducimos el sistema de ecuaciones a uno en el que aparece exclusivamente el campo eléctrico y que podrá ser resuelto con mayor o menor dificultad.

Esta relación constitutiva será dependiente de cada material concreto, y de sus propiedades fisicoquímicas. Podrá ser no-lineal (dependiente como una cierta potencia del campo, o mediante una función aun más complicada), incluir efectos de dispersión, de histéresis, etc.

Por ello, no es posible dar una solución general para la determinación del campo eléctrico en medios dieléctricos.

2 Definición

No obstante la posible generalidad de las relaciones constitutivas, se encuentra empíricamente que en la mayoría de los medios dieléctricos, cuando se aplica un campo electrostático de amplitud pequeña o moderada, la polarización resultante es simplemente proporcional al campo eléctrico

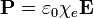
$\mathbf{P}=\varepsilon_0\chi_e\mathbf{E}\,$

A un material que verifica esta relación constitutiva se le denomina dieléctrico lineal. La cantidad adimensional $χ e$ es la denominada susceptibilidad eléctrica.

La relación constitutiva de los dieléctricos lineales nos dice que en ausencia de campo eléctrico la polarización es nula y que a medida que va aumentando el campo aplicado, aumenta la polarización en forma proporcional.

2.1 Medio anisótropo

En su forma más general, la susceptibilidad es un tensor, representable por una matriz, de forma que la relación constitutiva se escribirá

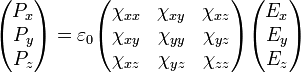
$\begin{pmatrix}P_x\\P_y\\P_z\end{pmatrix}=\varepsilon_0\begin{pmatrix}\chi_{xx} & \chi_{xy} & \chi_{xz}\\ \chi_{xy} & \chi_{yy} & \chi_{yz} \\ \chi_{xz} & \chi_{yz} & \chi_{zz}\end{pmatrix}\begin{pmatrix}E_x\\E_y\\E_z\end{pmatrix}$

Este tensor es simétrico, por lo que siempre se pueden elegir unos ejes ortogonales (denominados ejes principales), tales que la relación se convierta en una diagonal

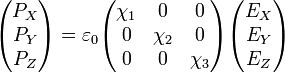
$\begin{pmatrix}P_X\\P_Y\\P_Z\end{pmatrix}=\varepsilon_0\begin{pmatrix}\chi_1 & 0 & 0\\ 0 & \chi_2 & 0 \\ 0 & 0 & \chi_3\end{pmatrix}\begin{pmatrix}E_X\\E_Y\\E_Z\end{pmatrix}$

Un material en el que se verifica esta forma de la relación lineal se denomina medio anisótropo, ya que en ellos, para un campo aplicado de la misma magnitud, el valor de la polarización depende de la dirección en que se aplique. En un medio anisótropo, además, la dirección de la polarización no será en general paralela al campo eléctrico, salvo que éste se aplique según uno de los ejes principales.

Muy pocos materiales presentan comportamiento anisótropo. Sólo algunos materiales cristalinos exhiben este comportamiento, ya que en un cristal es natural establecer diferencias entre una dirección y otra. En un medio fluido (líquido o gas) o en uno policristalino las diferencias entre una direcciones y otras desaparecen, y el material se convierte en isótropo.

2.2 Medio isótropo

En un medio isótropo, como son la mayoría, la constante de proporcionalidad es independiente de la dirección del campo eléctrico. En este caso, el tensor se reduce a un múltiplo de la matriz unidad, y la susceptibilidad se convierte en una cantidad escalar

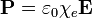
$\mathbf{P}=\varepsilon_0\chi_e\mathbf{E}$

Para campos electrostáticos, la susceptibilidad es siempre una cantidad positiva. Esto quiere decir que los dipolos que aparecen en el material, bien por inducción, bien por rotación de los ya existentes, se colocan en la dirección y sentido del campo aplicado.

3 Modelo microscópico

4 Permitividad

La relación constitutiva de un medio lineal se puede sustituir en la definición del vector desplazamiento

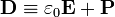
$\mathbf{D}\equiv\varepsilon_0\mathbf{E}+\mathbf{P}$

y resulta una nueva relación de proporcionalidad

$\mathbf{D}=\varepsilon_0(1+\chi_e)\mathbf{E}=\varepsilon_0\varepsilon_r \mathbf{E}=\varepsilon \mathbf{E}$

que establece que el desplazamiento eléctrico es proporcional al campo eléctrico. En esta relación aparecen dos nuevas cantidades, ambas denominadas permitividad o constante dieléctrica.

4.1 Permitividad relativa

Se define la permitividad relativa como

$\varepsilon_r = 1 + \chi_e$

En un medio anisótropo, es un tensor adimensional que da la proporcionalidad entre el desplazamiento y el campo.

En un medio isótropo es un escalar adimensional siempre mayor que la unidad (puesto que la susceptibilidad es siempre positiva)

$\chi_e>0\,$ $\Rightarrow$ $\varepsilon_r = 1 + \chi_e > 1$

Los valores típicos de la permitividad relativa varían desde cantidades muy próximas a la unidad, como en el caso de los gases nobles a valores mucho más grandes (caso de los plásticos o del agua):

Permitividad relativa
Material	$\varepsilon_r$	Material	$\varepsilon_r$
Agua	81	Aire	1.00054
Cuarzo	5.0	Argón	1.0052
Goma	3.0−4.0	Helio	1.000065
Mica	4.5−8.0	Neón	1.000123
Metacrilato	2.6−3.5	Oxígeno	1.00050

Hay que señalar que el agua no es en absoluto un dieléctrico ideal, por lo que el estudio de los campos en agua requiere necesariamente incluir los efectos de su conductividad.

La tabla anterior se refiere a la permitividad electrostática. Cuando tenemos campos variables en el tiempo (como una onda electromagnética que atraviesa un dieléctrico), la permitividad tiene un valor diferente, dependiente de la frecuencia del campo aplicado. A este efecto de dependencia con la frecuencia se denomina dispersión. Así, por ejemplo, para el agua, en el espectro visible, la permitividad relativa es 1.88, muy lejos del 81 estático.

4.2 Permitividad absoluta

La permitividad absoluta de un medio se define como

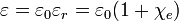
$\varepsilon = \varepsilon_0\varepsilon_r = \varepsilon_0(1+\chi_e)$

o, equivalentemente, la permitividad relativa es la proporción entre la absoluta y la permitividad del vacío

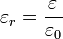
$\varepsilon_r = \frac{\varepsilon}{\varepsilon_0}$

De nuevo, en un medio anisótropo la permitividad absoluta es un tensor y en uno isótropo es una magnitud escalar. A diferencia de la relativa la permitividad absoluta es una cantidad dimensional. Se mide en las unidades que la permitividad del vacío, que en el sistema internacional son F/m.

La permitividad absoluta de una sustancia será siempre mayor que la del vacío, debido al signo de la susceptibilidad. Esto implica que la capacidad de un condensador relleno de dieléctrico es siempre mayor que la del mismo dieléctrico en vacío.

Normalmente, tanto a la permitividad absoluta como a la relativa se les suele quitar el “apellido” y se las denomina simplemente permitividad, a secas. La diferencia entre una y otra la da el contexto: la absoluta posee unidades, mientras que la relativa no, y en el sistema internacional la permitividad absoluta es siempre un número mucho menor que la unidad, mientras que la relativa es siempre mayor que 1. Así para el agua la permitividad relativa es 81 y la absoluta es 7×10^-10F/m.

5 Efecto de un campo sobre un dieléctrico lineal

5.1 Partícula en un campo externo

5.2 Condensador lleno de dieléctrico

6 Conductores en presencia de medios lineales

Cuando tenemos un conjunto de conductores inmersos en medios dieléctricos lineales e ideales, la distribución de campos posee muchas semejanzas con la del vacío.

En la mayoría de los casos, en el interior de un dieléctrico ideal no existen densidades de carga libre, ya que no han podido llegar hasta el interior, por no ser éste conductor. Por tanto, el vector desplazamiento es un campo solenoidal

$\nabla\cdot\mathbf{D}=\rho_l = 0\,$

Sustituyendo la relación constitutiva y el que el campo deriva del potencial escalar obtenemos la ecuación

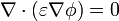
$\nabla\cdot(\varepsilon\nabla\phi)=0$

Esta no es la ecuación de Laplace, ya que la permitividad será una función de la posición, en general, y no puede salir de la derivada.

Si tenemos un medio homogéneo (o, al menos, homogéneo a trozos, esto es, que la permitividad es uniforme por regiones, por ejemplo, en un condensador tipo sandwich, con capas de dieléctrico), la ecuación sí se reduce a la de Laplace

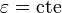
$\varepsilon = \mathrm{cte}$ $\Rightarrow$ $\nabla^2\phi=0$

Las condiciones de contorno para este problema son:

El potencial está fijado sobre la superficie de los conductores

$\phi = V_i\qquad\qquad\mathbf{r}\in S_i$

En las fronteras entre regiones la componente tangencial del campo eléctrico es continua

$\nabla\times[\mathbf{E}]=\mathbf{0}$

Esta condición implica que el potencial es una función continua.

En las fronteras entre regiones el salto en el vector desplazamiento es igual a la densidad superficial de carga libre,

$\mathbf{n}\cdot[\mathbf{D}]=\sigma_l$

A diferencia de lo que ocurre con las densidades volumétricas, no es raro que haya densidades superficiales de carga libre en las superficies de los dieléctricos. Existen diferentes mecanismos por los que puede depositarse carga en la superficie (por ejemplo, por fricción entre dieléctricos) y una vez almacenada permanece en esta superficie por la imposibilidad de fluir por el interior. Si se sabe que esta densidad es nula, la condición se reduce a la continuidad de la componente normal del vector desplazamiento.

$\sigma_l = 0\,$ $\Rightarrow$ $D_{1n}=D_{2n}\,$ $\Rightarrow$ $\varepsilon_1E_{n1}=\varepsilon_2 E_{n2}\,$

6.1 Ejemplo. El condensador plano

7 Energía en un medio lineal

8 Presión en un dieléctrico

9 Dependencia temporal. Dispersión

Dieléctrico lineal

De Laplace

Contenido

1 Introducción. Relaciones constitutivas

2 Definición

2.1 Medio anisótropo

2.2 Medio isótropo

3 Modelo microscópico

4 Permitividad

4.1 Permitividad relativa

4.2 Permitividad absoluta

5 Efecto de un campo sobre un dieléctrico lineal

5.1 Partícula en un campo externo

5.2 Condensador lleno de dieléctrico

6 Conductores en presencia de medios lineales

6.1 Ejemplo. El condensador plano

7 Energía en un medio lineal

8 Presión en un dieléctrico

9 Dependencia temporal. Dispersión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES