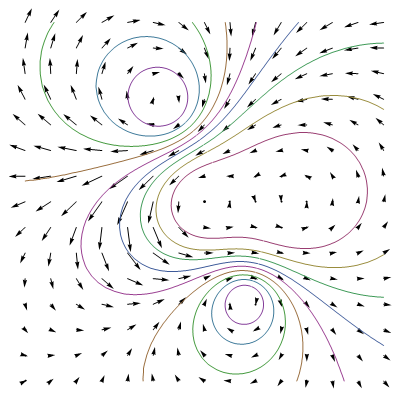
Líneas de campo
De Laplace
Contenido |
1 Definición
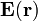, sus líneas de campo son las curvas que en cada punto son tangentes al valor del campo en dicho punto.
Matemáticamente, si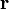 
es un punto de una línea de campo, y 
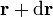es el siguiente punto a lo largo de la misma línea, se cumple que
Dos vectores son paralelos cuando son proporcionales, esto es
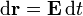
donde la constante de proporcionalidad debe ser diferencial, pues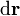 
es un vector de módulo diferencial y 
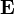no lo es. Podemos escribir esta relación como una ecuación diferencial
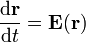
Podemos leer esta ecuación como que nos movemos a lo largo de la línea con una velocidad dada por el valor del campo en cada punto. El parámetro 
no es el tiempo, pero para interpretar los resultados podemos imaginárnoslo como tal
Esta ecuación diferencial es vectorial, lo cual quiere decir que en realidad contiene tres ecuaciones escalares acopladas, por ejemplo, en cartesianas
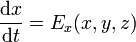
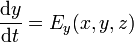
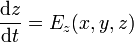
El que las ecuaciones sean acopladas implica que no pueden resolverse sucesivamente. Para hallar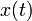 
precisamos de 
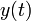y 
y viceversa. Por ello, en pocas ocasiones pueden determinarse analíticamente las ecuaciones de las líneas de campo, incluso en casos sencillos. Numéricamente, en cambio, suele ser un ejercicio sencillo.
2 Campo uniforme
El ejemplo más sencillo posible es el de un campo independiente de la posición,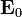 
. La ecuación de las líneas de campo es entonces
Estas son las ecuaciones vectoriales de una familia de rectas paralelas entre sí. El vector director de todas ellas apunta en la dirección del campo uniforme.
3 Campo central
4 Enlaces
- Siguiente: Derivada direccional
- Anterior:
