Péndulo simple (CMR)

De Laplace

Revisión a fecha de 15:59 3 dic 2019; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Movimiento plano
- 2.1 Puntos de equilibrio
3 Movimiento cónico
4 Caso general
5 Rotación forzada
6 Deducción alternativa del caso general
- 6.1 Empleando tres sistemas de referencia
- 6.2 Empleando coordenadas esféricas

1 Enunciado

Un péndulo simple está formado por una masa m unida a una varilla rígida de longitud 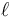$\ell$ , unida por su otro extremo a un punto fijo O mediante una articulación esférica. La masa está sometida a la acción del peso.

Considere, en primer lugar, el movimiento en un plano vertical. Determine la ecuación de movimiento para el ángulo θ que la varilla forma con la vertical. ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
Considere el caso de un péndulo cónico, el cual gira con velocidad angular constante 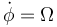$\dot{\phi}=\Omega$ alrededor del eje vertical. ¿Cuál debe ser la relación entre Ω y el ángulo con la vertical, θ, para que este movimiento sea posible? ¿Puede conseguirse un movimiento circular sea cual sea Ω?
Suponga ahora el movimiento general, en el cual puede cambiar tanto θ como el ángulo , de giro alrededor del eje vertical. A partir de la 2ª ley de Newton, obtenga las ecuaciones de movimiento para estos dos ángulos. Esto puede hacerse de diferentes maneras:
1. Empleando coordenadas esféricas.
2. Empleando un sistema de referencia en rotación alrededor del eje vertical, y empleando las fuerzas ficticias necesarias.
3. Considerando una composición de movimientos mediante tres sistemas de referencia: uno fijo “1”, uno intermedio “2” que gira alrededor del eje vertical un ángulo φ y uno ligado “3” que gira respecto a un eje horizontal un ángulo θ.
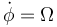Considerando el caso general, con movimiento en las dos coordenadas $\phi\,$ y θ, suponga que con un motor se fuerza a una rotación constante $\dot{\phi}=\Omega$ . En ese caso, ¿cómo queda la ecuación para θ? ¿Qué puntos de equilibrio hay? ¿Son estables o inestables?

2 Movimiento plano

El movimiento del péndulo en un plano es el caso clásico. La forma más simple de analizarlo es considerar un sistema de coordenadas polares, en las que

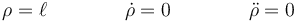
$\rho=\ell\qquad\qquad \dot{\rho}=0\qquad\qquad \ddot{\rho}=0$

y θ es el ángulo que el hilo forma con la vertical hacia abajo. Esto quiere decir que tomamos el eje OX vertical y hacia abajo y el eje OY horizontal en el plano de movimiento. El eje OZ será también horizontal y perpendicular al plano de movimiento.

La relación entre la base asociada a las coordenadas polares y la de las cartesianas es

$\left\{\begin{array}{rcl}\vec{u}_\rho&=&C\vec{\imath}+S\vec{\jmath}\\ \vec{u}_\theta&=&-S\vec{\imath}+C\vec{\jmath}\end{array}\right. \qquad\qquad \left\{\begin{array}{rcl}\vec{\imath}&=&C\vec{u}_\rho-S\vec{u}_\theta\\ \vec{\jmath}&=&S\vec{u}_\rho+C\vec{u}_\theta\end{array}\right.$

donde hemos usado la abreviatura, que emplearemos en lo que sigue:

$S=\mathrm{sen}(\theta)\qquad\qquad C=\cos(\theta)$

La segunda ley de Newton nos da, para el movimiento de la masa,

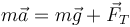
$m\vec{a}=m\vec{g}+\vec{F}_T$

Siendo el primer miembro, en polares,

$m\vec{a}=m(\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho+m(\rho\ddot{\theta}+2\dot{\rho}\dot{\theta})\vec{u}_\theta=-m\ell \dot{\theta}^2\vec{u}_\rho+m\ell\ddot{\theta}\vec{u}_\theta$

el peso

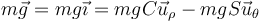
$m\vec{g}=mg\vec{\imath}=mgC\vec{u}_\rho-mgS\vec{u}_\theta$

y la tensión, cuyo módulo es desconocido,

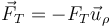
$\vec{F}_T=-F_T\vec{u}_\rho$

Sustituimos e igualamos componente a componente. Queda, para la componente radial

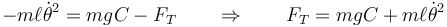
$-m\ell\dot{\theta}^2=mgC-F_T\qquad\Rightarrow\qquad F_T=mgC+m\ell\dot{\theta}^2$

y para la acimutal

$m\ell\ddot{\theta}=-mgS\qquad \Rightarrow\qquad \ddot{\theta}=-\frac{g}{\ell}\mathrm{sen}(\theta)$

Esta última es la conocida como ecuación del péndulo. La ecuación radial nos da la tensión, una vez calculado el ángulo como función del tiempo.

2.1 Puntos de equilibrio

Los puntos de equilibrio son aquellos en que si la velocidad inicial es nula, el sistema permanece en estado de reposo.

En este caso, estos son los puntos en que la aceleración angular es nula

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ddot{\theta}=0\qquad\Rightarrow\qquad \mathrm{sen}(\theta)=0\qquad \left{\begin{matrix}\theta=0 \\ \theta=\pi\end{matrix}\right.

Estos son el punto inferior (el péndulo en su posición normal) y el punto superior (péndulo invertido).

para analizar su estabilidad, consideramos desviaciones pequeñas respecto a estas posiciones de equilibrio.

Para $θ eq = 0$ tenemos

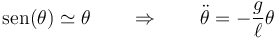
$\mathrm{sen}(\theta)\simeq \theta \qquad \Rightarrow\qquad \ddot{\theta}=-\frac{g}{\ell}\theta$

Esta es la ecuación de un oscilador armónico. Las soluciones son exponenciales imaginarias, lo que indica que la solución es oscilatoria alrededor de la posición de equilibrio y esta es estable.

Para $θ eq = π$ tenemos

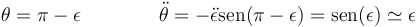
$\theta=\pi-\epsilon\qquad\qquad \ddot{\theta}=-\ddot{\epsilon} \mathrm{sen}(\pi-\epsilon)=\mathrm{sen}(\epsilon)\simeq \epsilon$

Lo que da la ecuación de movimiento aproximada

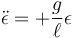
$\ddot{\epsilon}=+\frac{g}{\ell}\epsilon$

Esta ecuación tiene por soluciones exponenciales reales, lo que indica que la masa se aleja exponencialmente de la posición de equilibrio, y esta es inestable.

Péndulo simple (CMR)

De Laplace

Contenido

1 Enunciado

2 Movimiento plano

2.1 Puntos de equilibrio

3 Movimiento cónico

4 Caso general

5 Rotación forzada

6 Deducción alternativa del caso general

6.1 Empleando tres sistemas de referencia

6.2 Empleando coordenadas esféricas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES