Velocidad de arrastre en un hilo
De Laplace
1 Enunciado
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
2 Solución
La densidad de corriente en el hilo, si se distribuye uniformemente por sus sección será igual a
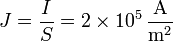
En un hilo metálico los únicos portadores de corriente son los electrones. Por ello, la densidad de corriente será igual a la densidad de carga de estos portadores multiplicada por su velocidad en la dirección de la corriente
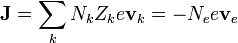


Cada átomo de plata contribuye con un electrón a la corriente. Por ello, el número de electrones de conducción por unidad de volumen coincide con el número de átomos de plata por unidad de volumen.
A su vez, podemos calcular la densidad numérica de átomos conociendo la masa atómica y la densidad de masa, ya que ésta será igual al número de átomos multiplicada por la masa de cada uno


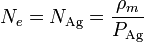
El peso de un átomo de plata es igual al peso atómico, expresado en kilogramos, dividido por el número de Avogadro. Reuniendo todo esto





