Energía magnética (GIE)
De Laplace
Contenido |
1 Corrientes de Foucault
Cuando se tiene un material metálico en el interior de un campo magnético variable en el tiempo se inducen corrientes de acuerdo con la ley de Faraday. En el caso de una espira, el resultado es una corriente a lo largo de ella, pero si tenemos un bloque de material lo suficientemente grande, pueden formarse líneas de corriente dentro del propio material. Estas corrientes describen circunferencias y otras curvas cerradas que no salen del material. Estas corrientes inducidas interiores se denominan corrientes de Foucault (o corrientes de remolino, “eddy currents” en inglés)
Podría pensarse que estas corrientes, al no fluir a lo largo de un circuito, no tienen efecto alguno, pero no es así. En primer lugar, generan calor por efecto Joule. Este calor es a menudo indeseable, ya que produce el calentamiento de partes de un sistema y debe ser desalojado. Un caso importante donde esto osucrre es en los núcleos de los transformadores. En un transformador las dos bobinas se montan sobre un núcleo de hierro. El campo magnético de las bobinas induce corrientes en el interior del hierro, calentándolo.
Para modelar este comportamiento se puede considerar un núcleo cilíndrico metálico a lo largo del cual existe un campo magnético variable en el tiempo de forma alterna
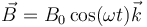
Dividiendo el volumen en espiras circulares y hallando la corriente inducida y, a partir de esta, la potencia disipada en cada una y la potencia total disipada (integrando todo el volumen) obtenemos un valor promedio
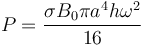
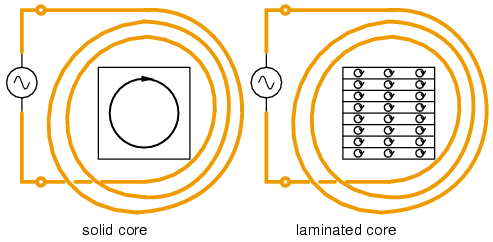
Este resultado muestra que las pérdidas aumentan como la cuarta potencia del radio. Esto implica que para un núcleo que tenga el doble de radio que otro, las pérdidas son 16 veces mayores. Para reducir este efecto los núcleos de los transformadores son laminados, ya que así se reduce el radio de cada capa.
No siempre este calor es indeseado. En las cocinas de inducción se emplea el mismo principio para calentar la comida.
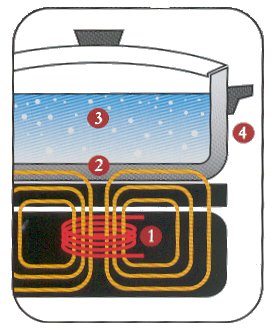
2 Frenos magnéticos
Como ilustración del efecto de las fuerzas magnéticas en el balance energético consideremos el caso de una espira que penetra en un campo magnético
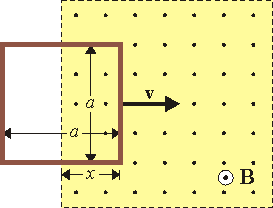
Supongamos en primer lugar que la espira se mueve con velocidad constante 
. En este caso, de acuerdo con la ley de Faraday, en la espira se induce una corriente (supuesta en sentido antihorario)
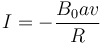
siendo R la resistencia de la espira. Ahora bien, la presencia de esta corriente produce calor por efecto Joule, siendo la potencia disipada
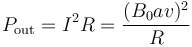
Esta energía se va principalmente en forma de calor. Si aquí aplicamos el primer principio de la termodinámica, podemos preguntarnos ¿de donde sale esta energía? Debe ser de una disminución de la energía total o de trabajo o calor que entran.
- De la energía total no es, pues la energía cinética permanece constante y la interna no está disminuyendo, ya que la espira no se está enfriando 8al contrario se está calentando, pues parte de esa potencia sirve para aumentar la temperatura de la espira)
- Tampoco del calor que entra, pues no está entrando calor alguno en la espira
- Debemos concluir entonces que procede de trabajo que está entrando. ¿Quién realiza este trabajo?
Si la espira se mueve a velocidad constante, por la segunda ley de Newton
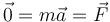
La fuerza neta sobre la espira debe ser nula. Sin embargo, sabemos que sobre una corriente rectilínea por la que circula una corriente y está dentro de un campo magnético aparece una fuerza
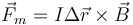
siendo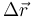 
el vector de posición relativo entre los extremos de la varilla. En este caso:
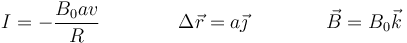
quedando la fuerza
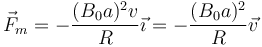
El campo magnético produce una fuerza opuesta al movimiento de la espira e intenta frenarla. Funciona como un rozamiento viscoso. Si la espira mantiene la velocidad constante es porque debe haber un agente externo empujando la espira. Alguien debe compensar la fuerza magnética de forma que
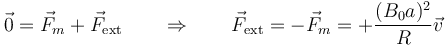
La potencia desarrollada por esta fuerza externa es
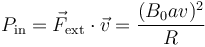
Vemos que coincide con la producción de calor por efecto Joule. Por tanto, vemos de donde sale la energía en este caso: procede del agente externo que está empujando la espira, el cual para mantener la velocidad constante debe realizar un trabajo sobre ella.
