Velocidad media en un movimiento armónico
De Laplace
1 Enunciado
Una partícula describe un movimiento armónico simple de frecuencia angular ω, pudiéndose mover a lo largo de una recta horizontal. En t = 0 pasa por la posición de equilibrio con una velocidad + v0.
- ¿Cuánto vale la velocidad media entre t = 0 y t = T / 4, con T el periodo de oscilación?
- ¿Cuánto vale la aceleración en t = T / 4?
2 Velocidad media
La velocidad media de una partícula en un movimiento rectilíneo se calcula como el cociente entre el desplazamiento neto y la duración del intervalo en que se realiza
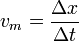
En este caso, el intervalo se nos da como dato: es la cuarta parte del periodo
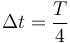
En un movimiento armónico simple, una partícula que parte del punto de equilibrio en t = 0 alcanza la máxima elongación en T / 4; en T / 2 vuelve a pasar por el origen en 3T / 4 alcanza la distancia máxima por el lado opuesto y en T regresa al origen, completando el ciclo.

Por tanto el desplazamiento entre t = 0 y t = T / 4 es igual a la elongación máxima, es decir a la amplitud.
y la velocidad media será igual a





