1.4. Arco capaz

De Laplace

Revisión a fecha de 17:43 13 sep 2013; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

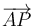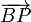Sean $A$ y $B$ dos puntos diametralmente opuestos en una circunferencia c. Sea $P$ otro punto de la misma circunferencia. Demuestre que los vectores $\overrightarrow{AP}$ y $\overrightarrow{BP}$ son ortogonales.

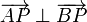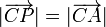Inversamente, sean $A$ , $B$ y $P$ tres puntos tales que $\overrightarrow{AP} \perp \overrightarrow{BP}$ . Sea $C$ el punto medio entre $A$ y $B$ . Pruebe que $|\overrightarrow{CP}| = |\overrightarrow{CA}|$ .

2 Solución

Para ver que son ortogonales calculamos el producto escalar de los dos vectores.

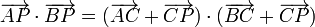
$\overrightarrow{AP}\cdot\overrightarrow{BP}=(\overrightarrow{AC}+\overrightarrow{CP})\cdot(\overrightarrow{BC}+\overrightarrow{CP})$

Desarrollando en esta expresión

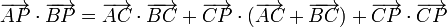
$\overrightarrow{AP}\cdot\overrightarrow{BP}=\overrightarrow{AC}\cdot\overrightarrow{BC}+\overrightarrow{CP}\cdot(\overrightarrow{AC}+\overrightarrow{BC})+\overrightarrow{CP}\cdot\overrightarrow{CP}$

Ahora bien, por ser puntos diametralmente opuestos, 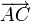$\overrightarrow{AC}$ y $\overrightarrow{BC}$ son vectores del mismo módulo $R$ , misma dirección y sentido contrario, por lo que

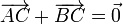
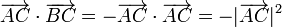
$\overrightarrow{AC}+\overrightarrow{BC} = \vec{0}$ $\overrightarrow{AC}\cdot\overrightarrow{BC}=-\overrightarrow{AC}\cdot\overrightarrow{AC}=-|\overrightarrow{AC}|^2$

lo que nos lleva a

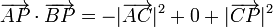
$\overrightarrow{AP}\cdot\overrightarrow{BP} = -|\overrightarrow{AC}|^2 + 0+|\overrightarrow{CP}|^2$

Puesto que A y P se encuentran sobre la circunferencia, equidistan del punto C:

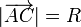
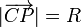
$|\overrightarrow{AC}|=R$ $|\overrightarrow{CP}|=R$

y por tanto

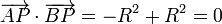
$\overrightarrow{AP}\cdot\overrightarrow{BP} = -R^2 + R^2 = 0$

El producto escalar es nulo y los vectores son, por tanto, ortogonales.

El resultado es independiente del punto $P$ , siempre que se encuentre sobre la circunferencia. A esta construcción se la denomina arco capaz.

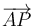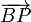Para el proceso inverso, se trata de ver que la situación es la misma, aunque la figura esté girada. Tenemos dos vectores $\overrightarrow{AP}$ y $\overrightarrow{BP}$ de los que sabemos que son ortogonales, esto es

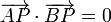
$\overrightarrow{AP}\cdot\overrightarrow{BP}=0$

Tenemos el punto C, que es el punto medio de A y B y por tanto verifica

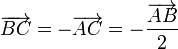
$\overrightarrow{BC}=-\overrightarrow{AC}=-\frac{\overrightarrow{AB}}{2}$

Se trata de demostrar que

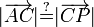
$|\overrightarrow{AC}| \stackrel{?}{=} |\overrightarrow{CP}|$

La demostración del enunciado recíproco es completamente análoga a la anterior. Operando exactamente como antes llegamos de nuevo a la igualdad

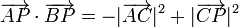
$\overrightarrow{AP}\cdot\overrightarrow{BP} = -|\overrightarrow{AC}|^2+|\overrightarrow{CP}|^2$

siendo ahora el dato que el primer miembro es nulo y por tanto

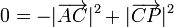
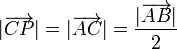
$0 = -|\overrightarrow{AC}|^2+|\overrightarrow{CP}|^2$ $\Rightarrow$ $|\overrightarrow{CP}|=|\overrightarrow{AC}|=\frac{|\overrightarrow{AB}|}{2}$

y por tanto el punto C se encuentra siempre a la misma distancia de P, siendo esta distancia igual a la mitad de la distancia entre A y B.

Esta construcción es útil en Mecánica. Imaginemos una escalera apoyada sobre una pared y el suelo. Cuando la escalera resbala, deslizándose sobre la pared y el suelo, ¿qué trayectoria describe el punto medio de la escalera? En este caso P es la esquina y A y B son los extremos de la escalera. C es su punto medio. Si L es la longitud de la escalera, este resultado prueba que 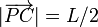$|\overrightarrow{PC}| = L/2$ y por tanto el punto C describe un arco de circunferencia.

1.4. Arco capaz

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES