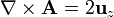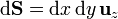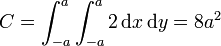Entrar Página Discusión Historial Go to the site toolbox

Cálculo de circulación

De Laplace

Contenido

1 Enunciado

Para el campo vectorial

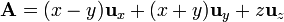
\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}

calcule su circulación a lo largo de las siguientes curvas cerradas:

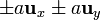  1. Un cuadrado de lado 2a, con vértices \pm a\mathbf{u}_{x}\pm a\mathbf{u}_{y}.
  2. Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas.
  3. Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas.

En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.

2 Solución

2.1 Cuadrado

La circulación a lo largo del cuadrado se compone de cuatro tramos, que calculamos por separado:

2.1.1 Primer Lado

Para el lado situado en x = a, z = 0,

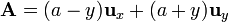
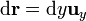
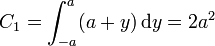
\mathbf{A} = (a-y)\mathbf{u}_{x}+(a+y)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{y}\mathbf{u}_{y}   \Rightarrow   C_1 = \int_{-a}^a (a+y)\,\mathrm{d}{y} = 2a^2

2.1.2 Segundo lado

Para el situado en y = a, z = 0

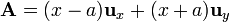
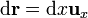
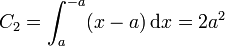
\mathbf{A} = (x-a)\mathbf{u}_{x}+(x+a)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}   \Rightarrow   C_2 = \int_{a}^{-a} (x-a)\,\mathrm{d}{x} = 2a^2

Nótese que no hace falta cambiar el signo a 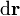\mathrm{d}{\mathbf{r}}, ya que el sentido de recorrido lo dan los límites de integración.

2.1.3 Tercer lado

Para el lado situado en x = − a, z = 0,

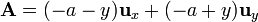
\mathbf{A} = (-a-y)\mathbf{u}_{x}+(-a+y)\mathbf{u}_{y}        

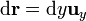
\mathrm{d}{\mathbf{r}}=\mathrm{d}{y}\mathbf{u}_{y}   \Rightarrow   

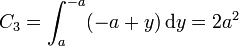
C_3 = \int_{a}^{-a} (-a+y)\,\mathrm{d}{y} = 2a^2

2.1.4 Cuarto lado

Para el situado en y = − a, z = 0

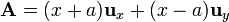
\mathbf{A} = (x+a)\mathbf{u}_{x}+(x-a)\mathbf{u}_{y}        

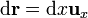
\mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}   \Rightarrow   

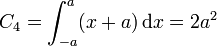
C_4 = \int_{-a}^{a} (x+a)\,\mathrm{d}{x} = 2a^2

2.1.5 Circulación

Sumando las cuatro contribuciones

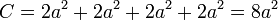
C = 2a^2+2a^2+2a^2+2a^2 = 8a^2\,

2.1.6 Aplicación del teorema de Stokes

Empleando el teorema de Stokes tenemos

\nabla\times\mathbf{A} = 2\mathbf{u}_{z}        

\mathrm{d}{\mathbf{S}} = \mathrm{d}{x}\,\mathrm{d}{y}\,\mathbf{u}_{z}   \Rightarrow   

C = \int_{-a}^a\int_{-a}^a 2\,\mathrm{d}{x}\,\mathrm{d}{y} = 8a^2

2.2 Circunferencia horizontal

2.3 Circunferencia vertical

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_circulaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace