Esfera rodeada de corona esférica

De Laplace

Revisión a fecha de 22:18 8 sep 2012; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Campo eléctrico
3 Potencial de la esfera interior
4 Energía electrostática
5 Conexión a tierra

1 Enunciado

Se tiene una esfera conductora de radio $a$ que almacena una carga $Q 0$ . Rodeándola se halla una corona esférica también conductora de radio interior $2 a$ y exterior $4 a$ . Esta corona se halla inicialmente aislada y descargada.

Calcule el campo eléctrico en todos los puntos del espacio. Puede suponerse que las distribuciones de carga son todas uniformes.
Determine el potencial al que se encuentra la esfera interior.
Calcule la energía electrostática almacenada en el sistema.
Suponga que se conecta la corteza exterior a tierra. Una vez que se vuelve al equilibrio electrostático, ¿cómo cambia el potencial de la esfera interior y la energía almacenada? ¿A qué se debe la diferencia de energía?

2 Campo eléctrico

Tenemos tres densidades de carga:

La que está en la esfera interior ( $r = a$ ): Esta, como indica el enunciado, almacena una carga total $Q 1 = Q 0$
La que está en la superficie del hueco ( $r = 2 a$ ): Por el teorema de Faraday, la carga en la pared del hueco debe ser igual a la encerrada cambiada de signo, es decir, vale $Q 2 = - Q 0$ .
La que está en la cara exterior de la corteza ( $r = 4 a$ ): En principio, esta podría tener cualquier valor, pero, dado que se nos dice que la corona está aislada y descargada, su carga total debe ser nula. Puesto que en la cara del hueco hay una carga $- Q 0$ , en la superficie exterior, para compensarla, debe haber una carga $Q 3 = + Q 0$

Puesto que se nos dice que cada una de las distribuciones es uniforme podemos hallar el campo aplicando la ley de Gauss. Tnemeos que en cada punto del espacio el campo eléctrico es radial y su módulo depende solo de la distancia al origen

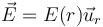
$\vec{E} = E(r)\vec{u}_r$

Considerando una superficie esférica de radio $r$ concéntrica con el sistema, se verifica

$\oint \vec{E}\cdot\mathrm{d}\vec{S}= \oint E(r)\,\mathrm{d}S = E(r)S = 4\pi r^2 E(r)$

De acuerdo con la ley de Gauss, esta flujo es proporcional a la carga encerrada por la superficie

$\oint \vec{E}\cdot\mathrm{d}\vec{S} = \frac{Q_\mathrm{int}(r)}{\varepsilon_0}\qquad\Rightarrow\qquad E(r) = \frac{Q_\mathrm{int}(r)}{4\pi \varepsilon_0 r^2}$

La carga encerrada depende del radio de la superficie que tomemos

Exterior de la corona: Encerramos toda la carga del sistema

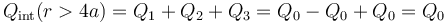
$Q_\mathrm{int}(r>4a) = Q_1+Q_2+Q_3 = Q_0-Q_0+Q_0 = Q_0\,$

y queda el campo

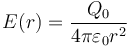
$E(r) = \frac{Q_0}{4\pi\varepsilon_0 r^2}$

Volumen de la corona: Encerramos la carga de la esfera interior y de la pared del hueco

$Q_\mathrm{int}(2a < r < 4a) = Q_1+Q_2 = Q_0-Q_0 = 0\,$

y queda el campo

E (r) = 0

3 Potencial de la esfera interior

4 Energía electrostática

5 Conexión a tierra

Esfera rodeada de corona esférica

De Laplace

Contenido

1 Enunciado

2 Campo eléctrico

3 Potencial de la esfera interior

4 Energía electrostática

5 Conexión a tierra

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES