Calor que escapa del cuerpo humano
De Laplace
1 Enunciado
Determine la cantidad de calor que escapa por cm² de piel del cuerpo humano si la piel se encuentra a 33 °C y el aire exterior se encuentra a 15 °C, estando el cuerpo cubierto por una sábana de algodón de 1 mm de espesor. ¿Y si además de la sábana está tapado con una manta de lana de 5 mm de espesor? La conductividad térmica de la lana es 0.03 W/m·K y la del algodón 0.04 W/m·K.
2 Solo una sábana
El flujo de calor a través de un medio sólido cumple la ley de Fourier
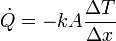
siendo k la conductividad térmica, A el área del material, Δx su espesor y ΔT la diferencia de temperaturas entre las dos caras.
En el caso de una sábana de algodón
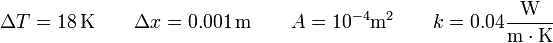
lo que nos da
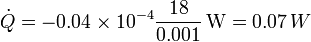
Esta cantidad parece pequeña, pero hay que considerar que se refiere a solo 1 cm² de piel. Cuando se considera toda la superficie que queda expuesta, se obtiene un flujo de calor muy importante, que debe ser compensado por el metabolismo.
3 Una sábana y una manta
Cuando tenemos dos capas puesta una a continuación de la otra se cumple

Las diferencias de temperaturas no son la misma en las dos capas. En la sábana será la diferencia entre la temperatura de la piel y la de contacto con la manta y en la manta entre el punto de contacto con la sabana y la temperatura exterior. Si Tm es la temperatura en el punto de contacto

cumpliéndose que los 18 K es la diferencia entre los extremos
El flujo de calor, en cambio, sí es el mismo en las dos capas, ya que todo el calor que sale del cuerpo termina fluyendo hacia el exterior

Podemos relacionar este flujo de calor con la diferencia total de temperaturas despejando

y sumando
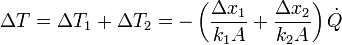
y obtenemos finalmente

Se llamamos resistencia térmica a los factores
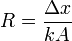
que miden la oposición al paso de calor. Para la sábana

y para la manta obtenemos un valor mucho mayor
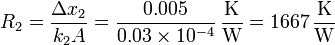
La ecuación anterior nos dice que la resistencia térmica total es la suma de las dos individuales
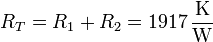
Resulta en este caso el flujo de calor






