Entrar Página Discusión Historial Go to the site toolbox

Magnitudes conservadas en un movimiento rectilíneo

De Laplace

Contenido

1 Enunciado

Una partícula de masa m = 2.00\,\mathrm{kg} se mueve según las leyes horarias, en el SI

x=(4.00+8.00t)\,\mathrm{m}\qquad\qquad y = (-2.00+1.00t)\,\mathrm{m}\qquad\qquad z = (-4.00-4.00t)\mathrm{m}

Demuestre que su cantidad de movimiento, su momento cinético respecto al origen de coordenadas y su energía cinética permanecen constantes. Halle el valor de estas tres cantidades.

2 Introducción

En lugar de sustituir directamente los diferentes valores numéricos, conviene expresarlos primero algebraicamente, ya que así ganan en generalidad.

A partir de las tres coordenadas de la partícula obtenemos su vector de posición en cada instante

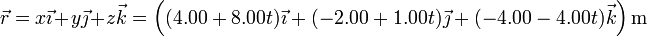
\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}=\left((4.00+8.00t)\vec{\imath}+(-2.00+1.00t)\vec{\jmath}+(-4.00-4.00t)\vec{k}\right)\mathrm{m}

Agrupando los términos que dependen del tiempo, podemos ver que esta posición corresponde a un movimiento rectilíneo y uniforme

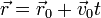
\vec{r}=\vec{r}_0+\vec{v}_0t

donde

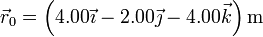
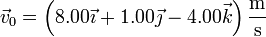
\vec{r}_0=\left(4.00\vec{\imath}-2.00\vec{\jmath}-4.00\vec{k}\right)\mathrm{m}        \vec{v}_0=\left(8.00\vec{\imath}+1.00\vec{\jmath}-4.00\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}

Al tratarse de un movimiento rectilíneo y uniforme, la aceleración de la partícula es nula y por tanto, la resultante de las fuerzas aplicadas de la partícula es también nula.

3 Cantidad de movimiento

La cantidad de movimiento de la partícula es igual al producto de su masa por su velocidad

\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\vec{v}_0\qquad\qquad \vec{p}=m\vec{v}=m\vec{v}_0

Al ser constante tanto la masa como la velocidad de la partícula, se conserva la cantidad de movimiento. Su valor es

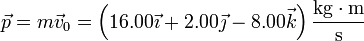
\vec{p}=m\vec{v}_0=\left(16.00\vec{\imath}+2.00\vec{\jmath}-8.00\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}

El que se conserve la cantidad de movimiento es también una consecuencia inmediata de que sobre la partícula la fuerza neta aplicada es nula.

4 Momento cinético

El momento cinético respecto al origen de coordenadas es igual al momento de su cantidad de movimiento

\vec{L}_O = \vec{r}\times\vec{p}=m\vec{r}\times\vec{v}

Sustituyendo la posición y la velocidad instantáneas

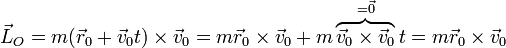
\vec{L}_O=m(\vec{r}_0+\vec{v}_0t)\times\vec{v}_0 = m\vec{r}_0\times\vec{v}_0+m\overbrace{\vec{v}_0\times\vec{v}_0}^{=\vec{0}}t = m\vec{r}_0\times\vec{v}_0

Vemos que el momento cinético también es constante, aunque la posición sea variable en el tiempo. La razón es que lo que varía es paralelo a la velocidad y por tanto se anula en el producto vectorial.

Esto está en completo acuerdo con que la fuerza aplicada es nula. Si la fuerza es nula,

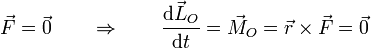
\vec{F}=\vec{0}\qquad\Rightarrow\qquad \frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O=\vec{r}\times\vec{F}=\vec{0}

El valor del momento cinético en este caso particular es

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{L}_O =m\vec{r}_0\times\vec{v}_0 = 2.00\left|\begin{\matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4.00 & -2.00 & -4.00\\ 8.00 & 1.0 0& -4.00\end{matrix}\right|\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}

5 Energía cinética

Obtenido de "http://tesla.us.es/wiki/index.php/Magnitudes_conservadas_en_un_movimiento_rectil%C3%ADneo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace