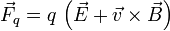Ecuaciones de Maxwell FII GIA
De Laplace
Contenido |
1 Introducción
Los fenómenos electromagnéticos que hemos visto hasta ahora se pueden explicar con cuatro leyes básicas. Estas leyes, en su expresión integral, son
1.1 Ley de Gauss
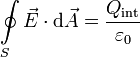
En esta ley se resumen varios datos sobre el campo eléctrico
- Las cargas eléctricas crean campo eléctrico.
- Las líneas de campo eléctrico mueren en las cargas positivas y mueren en las cargas negativas.
- El campo eléctrico se calcula a partir de la distribución de carga eléctrica.
1.2 Ley de Gauss magnética
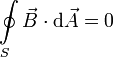
En esta ley se resumen varios datos sobre el campo magnético
- No existen cargas magnéticas.
- Las líneas de campo magnético son líneas cerradas.
1.3 Ley de Faraday
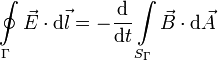
La letra Γ representa una línea cerrada, y SΓ es una superficie apoyada en esa línea.
En esta ley se expresa el hecho de que un campo magnético variable en el tiempo es capaz de producir un campo eléctrico. Por tanto, hay dos fuentes de campo eléctrico: las cargas eléctricas y un campo magnético variable en el tiempo.
1.4 Ley de Ampère
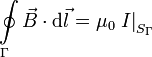
Aquí, Γ representa una línea cerrada y 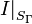 es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
Esta ley nos dice que
- Las corrientes eléctricas generan campos magnéticos.
- Las líneas de campo magnético generado por estas corrientes dan vueltas alrededor de las corrientes.
- El campo magnético se puede calcular a partir de la distribución de corriente eléctrica.
2 Corriente de desplazamiento
De las cuatro leyes que hemos visto en el apartado anterior, hay una de ellas que no es completamente correcta. Se trata de la ley de Ampère
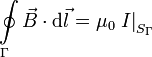
Esta ley dice que la circulación del campo magnético a lo largo de una curva cerrada Γ es igual a la corriente eléctrica que atraviesa una superficie SΓ que se apoye en esa curva. Sin embargo, para una curva cerrada cualquiera hay un número infinito de superficies que se apoyan en ella.
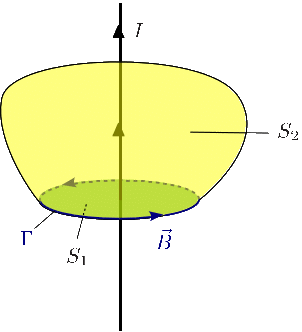
2.1 Hilo inifinito
Consideremos la situación de un hilo infinito por el que circula una corriente I. Escogemos como curva cerrada una circunferencia centrada en el hilo, que en cada punto es paralela al campo magnético. Las dos superficies de la figura se apoyan en la curva. La superfice S1 es el círculo definido por la circunferencia y la superfice S2 es una especia de boina amarilla.
Las dos superficies son atravesadas por la misma corriente, de modo que si consideramos la superficie S1 tenemos
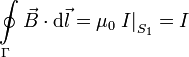
Mientras que si consideramos la superficie S2 tenemos
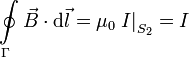
Es decir, en este caso la Ley de Ampère se cumple cualquiera que sea la superficie escogida.
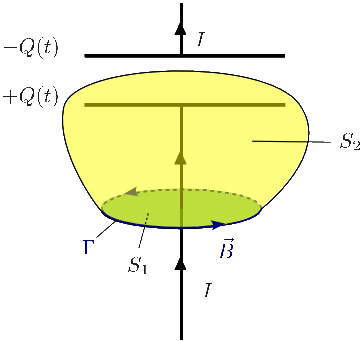
2.2 Hilo y condensador
Consideremos ahora la situación de la figura. El hilo está conectado a un condensador, de modo que la corriente I está depositando carga en las placas del condensador. Consideramos una situación en que la corriente depende del tiempo, pues en situación estacionaria el condensador actúa como un abierto y no puede haber corriente en el cable.
Observamos que en este caso la corriente no atraviesa la superficie S2, pues las cargas no se pueden mover en el interior del condensador. Si ahora aplicamos la Ley de Ampére en la superficie S1 tenemos
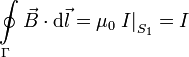
Mientras que si lo hacemos en la superficie S2 tenemos
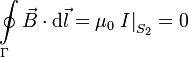
¿Como arreglamos esta discrepancia?
La ley de Ampère dice que las corrientes eléctricas crean campos magnéticos. El problema podría arreglarse si añadimos otro término al lado derecho de la Ley de Ampère, es decir, si encontramos otra fuente de campo magnético.
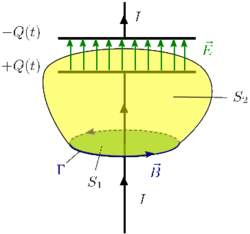
La pista la da la Ley de Faraday. Esta dice que un flujo magnético variable en el tiempo crea en el que campo eléctrico. Razonando por analogía, podemos postular que un flujo de campo eléctrico puede crear un campo magnético. De este modo, definimos la corriente de desplazamiento como
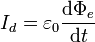
donde
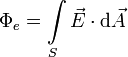
es el flujo del campo elétrico que atraviesa la superfice S. La ley de Ampére modificada queda así
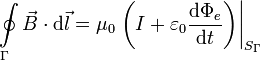
Ahora al aplicar la Ley de Ampère con la superfice S1 la corriente eléctrica que la atraviesa es I y el flujo eléctrico es nulo. Al aplicarla con la superficie S2 la corriente eléctrica que la atraviesa es nula mientras que la derivada del flujo eléctrico no lo es
En la superficie S1 tenemos
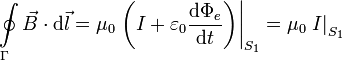
Mientras que si lo hacemos en la superficie S2 tenemos
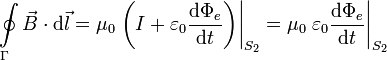
En el problema 2 del boletín vemos que los dos términos derechos son iguales.
La nueva versión de la ley se llama Ley de Ampère-Maxwell, en honor de James C. Maxwell, que enunció las ecuaciones que llevan su nombre.
Puede parecer que hemos demostrado la existencia de la corriente de desplazamiento, pero no es así. Hemos postulado que existe la corriente de desplazamiento. Sabemos que esta corriente existe porque la ley obtenida la introducirla (la Ley de Ampère-Maxwell) describe correctamente los hechos experimentales.
3 Ecuaciones de Maxwell
Podemos enunciar ahora las cuatro ecuaciones de Maxwell en su formulación integral
Ley de Gauss
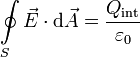
Ley de Gauss magnética
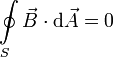
Ley de Faraday
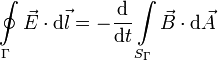
Ley de Ampère-Maxwell
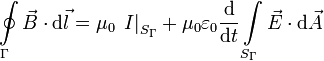
Los términos de la derecha de estas ecuaciones describen las fuentes que producen los campos que aparecen en los términos de la izquierda. Así, un campo eléctrico puede ser creado por cargas eléctricas (Ley de Gauss) o por un campo magnético variable en el tiempo (Ley de Faraday). Y un campo magnético puede ser creado por una corriente o por un campo eléctrico variable en el tiempo (Ley de Ampére-Maxwell).
Para completar la descripción teórica del Electromagnetismo hay que incluir la Ley de Lorentz, que describe la fuerza que los campo ejercen sobre las cargas eléctricas. Así, la fuerza que una carga puntual q con velocidad  sufre cuando se mueve bajo la acción de un campo eléctrico y campo magnético es
sufre cuando se mueve bajo la acción de un campo eléctrico y campo magnético es