6.9. Placa en escuadra rotatoria

De Laplace

1 Enunciado

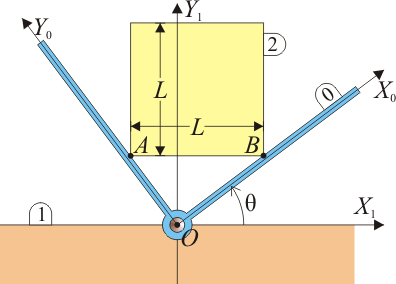
Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo θ(t) que forma la barra OX₀ con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vértices inferiores, A y B, una placa cuadrada de lado L, cuyo lado inferior AB mantiene en todo momento su horizontalidad respecto al plano “1”.

1. En función del ángulo θ, localice geométricamente de forma razonada el centro instantáneo de rotación del movimiento {20}. Exprese su vector de posición relativo al punto O tanto en la base ligada al sólido “0” como en la ligada al sólido “1”. ¿Dónde se localiza el CIR del movimiento {21}?
2. En función de θ y de , calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B.

2 Centro instantáneo de rotación

2.1 Posición del CIR {20}

Localizamos la posición del CIR I₂₀ a partir de la velocidad de dos puntos en dicho movimiento. En este caso, lo más sencillo es considerar los dos puntos de contacto A y B.

En estos dos puntos se cumple que la placa no puede atravesar a la escuadra y por tanto la velocidad de los puntos A y B debe ser tangencial a las barras de la escuadra, esto es, respectivamente a lo largo de los ejes OX₀ y OY₀

2.2 Expresión en la base “0”

2.3 Expresión en la base “1”

2.4 Localización del CIR {21}

3 Velocidades de deslizamiento