5.7. Movimiento relativo de dos ventiladores
De Laplace
Contenido |
1 Enunciado
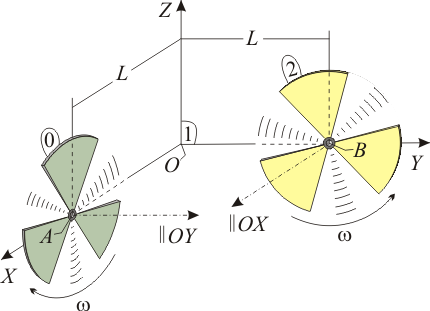
Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos “0” y “2”) de orientación fija, ambos a la misma altura, y con sus respectivos centros (A y B) equidistantes (distancia L) de la esquina (punto O). Los dos ventiladores rotan con velocidad angular de módulo constante igual a ω, si bien lo hacen con las orientaciones y sentidos respectivamente indicados en la figura. Definido el triedro fijo OXYZ (sólido “1”) del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determine
-
 y
y 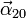
-
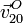 y
y 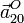 ;
;
- El eje instantáneo de rotación (E.I.R.) del movimiento {20}.
Nota: Se recomienda la utilización del triedro “1” para la descomposición del movimiento-problema, así como el uso de su base vectorial para resolver el ejercicio.
2 Velocidad y aceleración angular
2.1 Velocidad angular
En este caso tenemos la descomposición
La velocidad angular es la suma de las de los dos movimientos relativos
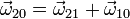
La velocidad angular del movimiento {21} va en la dirección del eje OX
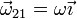
La del movimiento {10} es igual en magnitud, y de sentido opuesto a la del movimiento {01}, que es el dato que se nos da
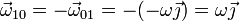
por lo que la velocidad angular absoluta vale
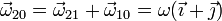
2.2 Aceleración angular
Para las aceleraciones angulares tenemos la ley de composición
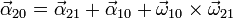
La aceleración angular del movimiento {21} es nula, por ser una rotación con velocidad angular constante
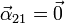
Lo mismo ocurre con la del movimiento {10}, ya que en este movimiento, el ventilador 0 “ve” al sistema “1” rotar con velocidad angular constante alrededor de un eje fijo
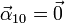
Las velocidades angulares que aparecen en el último término son vectores ya conocidos, por lo que
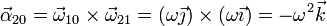
3 Velocidad y aceleración
3.1 Velocidad
La velocidad del punto O en el movimiento {20} se puede descomponer como

La velocidad de O en el movimiento {21} es la de una rotación en torno a un eje que pasa por B

La velocidad del mismo punto en el movimiento {10} es otra rotación, en este caso en torno a un eje que pasa por A
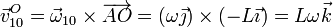
Sumando las dos contribuciones
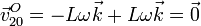
El punto O se encuentra en reposo instantáneo en el movimiento {20}.





