Descarga de un condensador

De Laplace

Revisión a fecha de 19:38 10 jun 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Entre dos placas planas y paralelas, perfectamente conductoras, de sección $S$ , y separadas una distancia $a$ se encuentra un medio resistivo, de permitividad $\varepsilon$ y conductividad $σ$ . Entre las placas hay establecida una tensión $V 0$ .

Halle la corriente que circula entre las placas y la carga almacenada en cada una, así como la energía almacenada en el sistema.
En $t = 0$ se desconecta el generador. Determine la evolución de la carga en las placas a partir de ese momento.
Halle la energía disipada en el medio durante el proceso de descarga del condensador.
Describa el comportamiento del sistema mediante un circuito equivalente.

2 Solución

2.1 Estado estacionario previo a la desconexión

En el estado estacionario, las ecuaciones que describen el sistema son

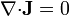
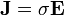
$\nabla{\cdot}\mathbf{J}=0$ $\nabla\times\mathbf{E}=\mathbf{0}$ $\mathbf{J}=\sigma\mathbf{E}$

Si suponemos que la corriente va en la dirección perpendicular a las placas

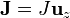
$\mathbf{J}=J\mathbf{u}_{z}$

el valor de la densidad resulta ser uniforme

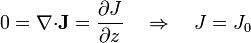
$0=\nabla{\cdot}\mathbf{J}=\frac{\partial J}{\partial z}\quad\Rightarrow\quad J=J_0$

El valor de esta constante lo determinamos a partir del campo eléctrico y la diferencia de potencial

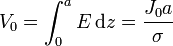
$\mathbf{E}=\frac{\mathbf{J}}{\sigma}=\frac{J_0}{\sigma}\mathbf{u}_{z}$ $V_0=\int_0^aE\,\mathrm{d}z=\frac{J_0a}{\sigma}$

de donde

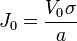
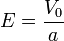
$J_0=\frac{V_0\sigma}{a}$ $E=\frac{V_0}{a}$

Conocida la densidad de corriente podemos calcular la corriente que atraviesa el material. Para ello consideramos una sección paralela a una de las placas

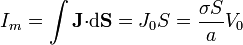
$I_m=\int \mathbf{J}{\cdot}\mathrm{d}\mathbf{S}=J_0S=\frac{\sigma S}{a}V_0$

En el estado estacionario, la corriente $I$ que llega por el cable (y que es la que podemos medir mediante un amperímetro) equivale a la que fluye por el material,

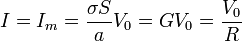
$I=I_m=\frac{\sigma S}{a}V_0=GV_0=\frac{V_0}{R}$

Desde el punto de vista de la medida de la corriente, el sistema se comporta como una resistencia para una tensión continua.

El hecho de que en el interior del elemento exista un campo eléctrico mientras que en el exterior sea (aproximadamente) nulo, implica la presencia de una carga superficial en las placas, con densidad

$\sigma_s=\mathbf{n}{\cdot}[\mathbf{D}]=\pm\frac{\varepsilon V_0}{a}$

siendo el signo positivo el correspondiente a la placa a mayor potencial.

En el volumen óhmico no hay carga, por ser el material homogéneo y el estado estacionario

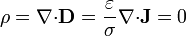
$\rho=\nabla{\cdot}\mathbf{D}=\frac{\varepsilon}{\sigma}\nabla{\cdot}\mathbf{J}=0$

La carga total acumulada sobre la placa positiva es

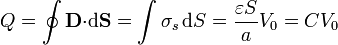
$Q=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=\int \sigma_s\,\mathrm{d}S=\frac{\varepsilon S}{a}V_0=CV_0$

La carga acumulada corresponde a la de un condensador de capacidad $C\,$ .

Podemos preguntarnos cómo es posible que, pudiendo la carga moverse por el interior del material, permanezca una cierta cantidad almacenada en las placas. La respuesta es que esta carga no es siempre la misma. Efectivamente la carga de las placas atraviesa el material, atraída por las de signo opuesto situadas al otro lado. Pero, al estar el sistema conectado a un generador, éste va reponiendo la carga de las placas, de forma que aunque individualmente no son las mismas, su cantidad neta sí permanece constante.

2.2 Evolución de la carga en las placas

2.3 Potencia disipada y balance energético

2.4 Circuito equivalente

Descarga de un condensador

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Estado estacionario previo a la desconexión

2.2 Evolución de la carga en las placas

2.3 Potencia disipada y balance energético

2.4 Circuito equivalente

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES