Problemas de cinemática del sólido rígido (G.I.T.I.)
De Laplace
Revisión a fecha de 20:18 2 ago 2010; Antonio (Discusión | contribuciones)
1 Ejemplo de campo de velocidades de un sólido
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,
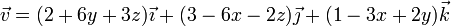
- Pruebe que corresponde al movimiento de un sólido rígido.
- Determine la velocidad angular y la velocidad de deslizamiento.
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.
2 Velocidad de tres puntos de un sólido
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
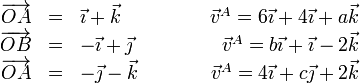
- Halle los valores de a, b, c.
- Halle la velocidad del punto
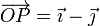 .
.
- Calcule la velocidad angular y la de deslizamiento
- Determine la posición del eje instantáneo de rotación y mínimo deslizamiento.





