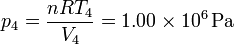Caso práctico de ciclo de Stirling
De Laplace
Contenido |
1 Enunciado
100 moles de gas ideal diátomico sufre un ciclo de Stirling internamente reversible, representado en la figura. El ciclo se compone de dos isotermas y dos isócoras. Las temperaturas de trabajo son 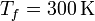 y
y 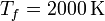 , mientras que las presiones extremas son
, mientras que las presiones extremas son 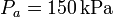 y
y 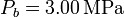 .
.
- En cada uno de los procesos, calcula la variación de energía interna, el trabajo realizado y el calor absorbido por el gas. Calcula el rendimiento del ciclo.
- Calcula la variación de entropía en cada proceso del ciclo y la variación neta en el ciclo completo.
- Compara el rendimiento del ciclo con el de una máquina de Carnot reversible que trabaje entre las mismas temperaturas.
- Imagina y describe un experimento que te permita recorrer el ciclo.
Dato: 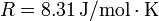
2 Intercambios energéticos
2.1 Presiones, volúmenes y temperaturas
Antes de calcular el trabajo y el calor en cada proceso, vamos a hallar la presión, la temperatura y el volumen en cada uno de los vértices del ciclo, ya que necesitaremos estos datos más adelante.
2.1.1 Estado inicial 1
Para el estado “1” conocemos tanto su presión y su temperatura
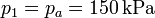

El volumen que ocupa el gas lo obtenemos sabiendo el número de moles de gas:
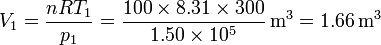
Nótese que, dado que estamos trabajando en el sistema internacional, el volumen resultante aparece en m³.
2.1.2 Estado 3
Para el estado 3 también conocemos tanto la presión como la temperatura
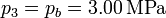
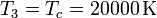
Obtenemos el volumen de la misma manera
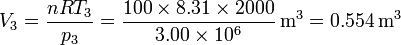
2.1.3 Estado 2
Para el final de la compresión isoterma, observamos que su temperatura es la misma que la del estado 1 y su volumen el mismo del estado 3

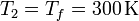
Con estos dos datos obtenemos la presión
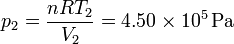
2.1.4 Estado 4
Por último, para el final de la expansión isoterma, aplicamos que su temperatura es la misma que la del estado 3 y su volumen el mismo del estado 1

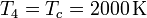
Con estos dos datos obtenemos la presión