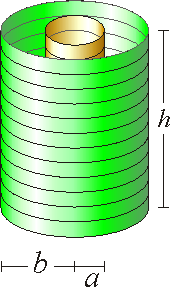
Inducción mutua de dos solenoides cilíndricos

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Matriz de inducciones mutuas 2.1.1 Cálculo a partir de la energía 2.1.2 Cálculo a partir de los flujos 2.2 Constante de acoplamiento 2.3 Asociación en serie 2.4 Asociación en paralelo

1 Enunciado

Dos solenoides cilíndricos muy largos se disponen concntricamente. Dichos solenoides poseen la misma longitud y número de espiras N₁ y N₂, respectivamente, las cuales están arrolladas en el mismo sentido. Los radios de las bobinas son, respectivamente, a y b (a < b).

1. Determine la matriz de inducciones mutuas del sistema.
2. Calcule la constante de acoplamiento entre las bobinas.
3. Suponga que se conectan el extremo superior de la bobina interior con el extremo superior de la exterior. ¿Cuál es la autoinducción equivalente de la asociación?
4. Suponga que se conectan en paralelo, ¿cuál es la autoinducción equivalente de la asociación?

2 Solución

2.1 Matriz de inducciones mutuas

Existen tres métodos a la hora de calcular los coeficientes de inducción mutua y autoinducción. Uno es el cálculo directo a partir de la fórmula de Neumann, que no consideraremos por ser extremadamente complicado. El segundo es partir del flujo inducido en cada solenoide por los campos magnéticos propios o ajenos. El tercero es a partir de la expresión de la energía magnética.

Comenzaremos por este último, que es el más sencillo, y luego repetiremos el problema a partir de los flujos.

2.1.1 Cálculo a partir de la energía

Es conocido que un solenoide muy largo de longitud h, radio R, con N espiras por las cuales circula una corriente I produce un campo magnético

• Si ρ < R

• Si ρ > R

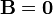
En nuestro caso disponemos de dos solenoides, cada uno de los cuales crea su propio campo magnético. Por simple aplicación del principio de superposición resulta

• Si ρ < a

• Si a < ρ < R

• Si b < ρ

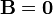
donde I₁, e I₂ son las corrientes que circulan por los solenoides de radios a y b, respectivamente. Aquí hemos hecho uso de que todas las bobinas poseen la misma longitud y el mismo sentido de giro (lo que hace que todos los campos tengan el mismo sentido).

Una vez conocido el campo podemos obtener la energía magnética almacenada a partir de la expresión

Conocido que el campo es uniforme por regiones podemos escribir esta integral como

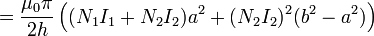
Desarrollando esta expresión resulta

Comparando este resultado con

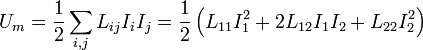
resulta la matriz de inducciones mutuas

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathsf{L}=\frac{\mu_0\pi{h}\left(\begin{array}{cc}N_1^2a^2 & N_1N_2a^2 \\ N_1N_2a^2 &N_2b^2\end{array}\right)

Esta matriz es simétrica, como era de esperar.

2.1.2 Cálculo a partir de los flujos

2.2 Constante de acoplamiento

2.3 Asociación en serie

2.4 Asociación en paralelo