Movimiento armónico simple

De Laplace

Revisión a fecha de 20:06 7 feb 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Combinación de funciones trigonométricas
3 Amplitud y fase
4 Amplitud compleja

1 Introducción

El movimiento armónico simple (o, abreviadamente, M.A.S.) es el descrito por una partícula que se mueve a lo largo de una recta verificando la ley de Hooke

$\mathbf{F} = - k\mathbf{r}\,$

Por tratarse de un movimiento rectilíneo, puede reducirse el movimiento a una sola componente

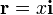
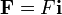
$\mathbf{r}=x\mathbf{i}$ $\mathbf{F}=F\mathbf{i}\,$

de forma que la ecuación de movimiento se reduce a

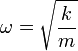
$\ddot{x}= -\frac{k}{m}x=-\omega^2x$ $\omega=\sqrt{\frac{k}{m}}$

La solución de esta ecuación diferencial, con las condiciones iniciales

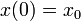
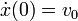
$x(0)=x_0\,$ $\dot{x}(0)=v_0$

es la forma general de un movimiento armónico simple.

2 Combinación de funciones trigonométricas

Para resolver la ecuación de movimiento de un oscilador armónico, empleando técnicas elementales, observamos que trata de hallar una función cuya segunda derivada sea proporcional a la propia función. Es fácil encontrar dos funciones que cumplen esta condición

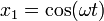
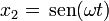
$x_1 = \cos(\omega t)\,$ $x_2 = \,\mathrm{sen}(\omega t)$

Por simple sustitución comprobamos que se cumple

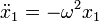
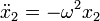
$\ddot{x}_1 = -\omega^2x_1$ $\ddot{x}_2 = -\omega^2x_2$

Ninguna de estas dos soluciones particulares puede ser la solución general, ya que no cumplen las condiciones iniciales del movimiento. Sin embargo, una combinación lineal de ellas sí lo es. Multiplicando cada una por una constante y sumando, tenemos que

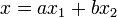
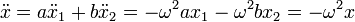
$x = ax_1 + bx_2\,$ $\Rightarrow$ $\ddot{x}=a\ddot{x}_1+b\ddot{x}_2 = -\omega^2ax_1-\omega^2 b x_2 = -\omega^2x$

El valor de estas dos constantes, $a$ y $b$ lo dan las condiciones iniciales. Al resultar un sistema de dos ecuaciones con dos incógnitas, la solución queda completamente determinada. Por tanto, la forma general del movimiento armónico simple es

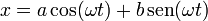
$x = a\cos(\omega t) + b\,\mathrm{sen}(\omega t)$

Derivando esta ecuación obtenemos la velocidad instantánea

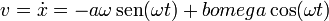
$v =\dot{x}= -a\omega\,\mathrm{sen}(\omega t)+bºomega\cos(\omega t)$

Imponiendo las condiciones iniciales obtenemos $a$ y $b$ . De la posición inicial

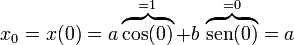
$x_0 = x(0) = a\overbrace{\cos(0)}^{=1} + b\,\overbrace{\mathrm{sen}(0)}^{=0} = a$ $\Rightarrow$ $a = x_0\,$

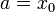
y de la velocidad inicial

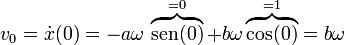
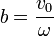
$v_0 = \dot{x}(0) = -a\omega\,\overbrace{\mathrm{sen}(0)}^{=0} + b\omega\overbrace{\cos(0)}^{=1} = b\omega$ $\Rightarrow$ $b = \frac{v_0}{\omega}$

con lo que la solución general, en función de la posición y la velocidad inicial es

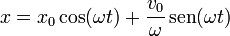
$x = x_0\cos(\omega t) + \frac{v_0}{\omega}\,\mathrm{sen}(\omega t)$

3 Amplitud y fase

Una forma alternativa de escribir la solución general del movimiento armónico simple es

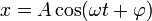
$x = A\cos(\omega t+\varphi)$

donde $A$ y $\varphi$ son dos constantes que se pueden obtener a partir de las condiciones iniciales. Estas dos constantes, dada su importancia, poseen nombre propio:

Amplitud: A la constante $A$ se la denomina amplitud del movimiento. Nos da elongación máxima que puede alcanzar la partícula desde su posición central

Constante de fase: A la combinación 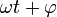$\omega t + \varphi$ se la denomina fase del movimiento. Nos indica en qué punto del periodo de oscilación nos encontramos. La cantidad $\varphi$ se la denomina constante de fase. Nos informa del desfase entre el estado de oscilación de la partícula y el que tendría un oscilador de referencia que en $t = 0$ tuviera fase nula.

4 Amplitud compleja

Movimiento armónico simple

De Laplace

Contenido

1 Introducción

2 Combinación de funciones trigonométricas

3 Amplitud y fase

4 Amplitud compleja

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES