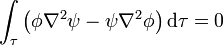Coeficientes de capacidad
De Laplace
(→Demostración) |
(→Demostración) |
||
| Línea 120: | Línea 120: | ||
<center><math>\int_\tau\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\mathrm{d}\tau=\oint_{\partial\tau}\left(\phi\nabla\psi-\psi\nabla\phi\right)\cdot\mathrm{d}\mathbf{S}</math></center> | <center><math>\int_\tau\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\mathrm{d}\tau=\oint_{\partial\tau}\left(\phi\nabla\psi-\psi\nabla\phi\right)\cdot\mathrm{d}\mathbf{S}</math></center> | ||
| + | |||
| + | Si en esta identidad hacemos <math>\phi=\phi_i</math> y <math>\psi=\phi_k</math>, dos de las funciones base, el primer miembro se anula ya que ambas verifica la ecuación de Laplace en el espacio entre los conductores | ||
| + | |||
| + | <center><math>\nabla^2\phi=\nabla^2\phi_k=0\,</math>{{tose}}<math>\int_\tau\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\mathrm{d}\tau=0</math></center> | ||
==Casos particulares== | ==Casos particulares== | ||
Revisión de 17:46 17 ene 2010
Contenido |
1 Problema del potencial
Cuando se tiene un sistema de conductores Sk a diferentes potenciales Vk, y quiere determinarse la distribución de potencial eléctrico y de campo eléctrico entre ellos, debe resolverse el problema del potencial:

con las condiciones de contorno
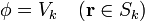
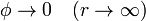
Suponemos que la única carga se encuentra sobre los conductores, y no en el espacio entre ellos; por ello, la ecuación diferencial es la de Laplace y no la de Poisson. La condición de contorno en el infinito puede ser sustituida por una en una superficie exterior que rodee al sistema (porque tengamos, por ejemplo, un sistema de conductores dentro de una jaula de Faraday).
La solución de este problema permite hallar el campo eléctrico entre los conductores, la carga en cada conductor, y la energía almacenada, entre otras cantidades. Aunque puede demostrarse que existe solución y es única, ello no quiere decir que sea sencilla de calcular. En muy pocos casos existe solución analítica y a menudo es preciso recurrir a una solución numérica.
2 Solución del problema del potencial
El problema del potencial tiene una complicación adicional aparte de su complejidad matemática: depende de los potenciales de todos los conductores. Esto quiere decir que si se modifica el potencial de uno solo de ellos, aunque el resto permanezca a la misma tensión que estaba, ya la solución completa es distinta, y todos los valores previos de campos, cargas o energía, se ven modificados.
Interesa entonces saber si existe un principio de superposición que permita separar el efecto de un conductor del del resto.
Quede claro que la solución del problema completo no es la suma de las soluciones que habría si estuviera cada conductor y no estuviera el resto. La presencia de nuevos conductores en un sistema, perturba a los ya existentes, redistribuyendo sus cargas, de forma que el campo que produce cada uno ya no es el mismo que producían antes de esta introducción.
No obstante lo anterior, sí podemos escribir la solución del problema del potencial (en ausencia de carga de volumen) como una combinación lineal de soluciones
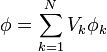
donde los Vk son las tensiones de los diferentes conductores y las 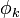 son funciones base definidas por el problema del potencial
son funciones base definidas por el problema del potencial
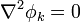
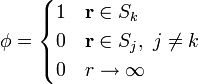
Expresado en palabras, la función 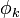 representa el potencial que habría si el conductor k estuviera a potencial unidad y el resto de los conductores estuviera a tierra (pero presentes).
representa el potencial que habría si el conductor k estuviera a potencial unidad y el resto de los conductores estuviera a tierra (pero presentes).
Puede demostrarse que esta expresión es solución sustituyendo en el problema del potencial original y aplicando el teorema de unicidad.
La ventaja que trae el expresar la solución como una combinación lineal de funciones base es que estas funciones base son independientes de los potenciales concretos a los que se encuentran los diferentes conductores. Solo dependen de la geometría del sistema. Por ello, si se modifica la tensión de uno solo de los conductores, no es preciso recalcular la solución completa; basta con modificar el coeficiente correspondiente en la combinación lineal.
3 Cargas en los conductores
A menudo, lo que interesa no es determinar la distribución de potencial en todo el espacio, sino simplemente las cargas en los diferentes conductores. Esto se suele hacer hacer en el proceso de conversión de un sistema complejo en una caja negra, en la cual se da una serie de datos (los potenciales) y se obtienen los resultados (las cargas) sin necesidad de conocer el funcionamiento interno.
La carga en cada conductor puede hallarse mediante la ley de Gauss
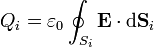
siendo Si una superficie cerrada que envuelve al conductor i. Aplicando ahora la combinación lineal de funciones base, queda, para el campo eléctrico
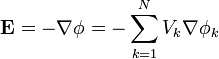
y para la carga en el conductor i
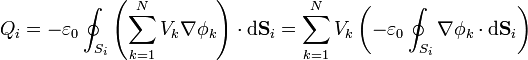
o, de forma más concisa
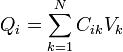
donde
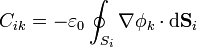
son los llamados coeficientes de capacidad e inducción, que describiremos más en detalle más adelante.
Esta relación nos dice que las cargas en los conductores se pueden expresar como una combinación lineal de las diferentes tensiones. La relación se puede expresar en forma matricial
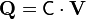
donde 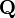 y
y 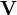 son vectores columna de N elementos, con las cargas y tensiones respectivamente y
son vectores columna de N elementos, con las cargas y tensiones respectivamente y  es una matriz
es una matriz 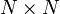 formada por los coeficientes de capacidad e inducción.
formada por los coeficientes de capacidad e inducción.

Como en el caso de la solución del problema del potencial completo, la modificación de uno de los potenciales no afecta a la matriz de coeficientes de capacidad e inducción. Sí cambia, en egeneral, el valor de todas las cargas, de acuerdo con la relación anterior.
4 Coeficientes de capacidad e inducción
4.1 Definición e interpretación
Los coeficientes de capacidad e inducción se definen con la fórmula general
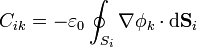
donde se distinguen:
- Coeficientes de capacidad
- cuando i = k, esto es, los elementos de la diagonal principal de la matriz
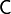 .
.
- Coeficientes de inducción
- cuando
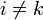 , es decir, los elementos sobre y bajo la diagonal principal de
, es decir, los elementos sobre y bajo la diagonal principal de 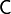 .
.
En términos físicos:
- el coeficiente de capacidad Cii es la carga por unidad de potencial que aparece en el conductor i cuando dicho conductor está a potencial unidad y el resto de los conductores están a tierra.
- el coeficiente de capacidad Cik es la carga por unidad de potencial que se induce en el conductor i cuando el conductor k está a potencial unidad y el resto de los conductores (incluyendo el i) están a tierra.
4.2 Unidades
Dado que relacionan un potencial con una carga, tanto los coeficientes de capacidad como los de inducción se miden en Faradios
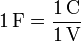
Sin embargo, en la mayoría de las situaciones prácticas, un faradio es una unidad gigantesca. Por ello, es mucho más frecuente emplear picofaradios o nanofaradios.
4.3 Simetría
Los coeficientes de inducción son simétricos, esto es,
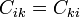
en palabras: la carga que se induce en el conductor i cuando el k está a potencial unidad y el resto a tierra, es la misma que se induce en el conductor k cuando es el i el que está a potencial unidad y el resto a tierra. Este resultado puede parecer un poco antiintuitivo, pues puede ocurrir que el conductor i sea de tamaño gigantesco, y el k diminuto, y aun así su influencia mutua será la misma (en un caso al conductor pequeño le cabe muy poca carga, y en el otro, produce muy poco efecto, induciendo muy poca carga en el grande.
4.3.1 Demostración
La simetría de los coeficientes de inducción es una consecuencia de la segunda identidad de Green:

Si en esta identidad hacemos φ = φi y ψ = φk, dos de las funciones base, el primer miembro se anula ya que ambas verifica la ecuación de Laplace en el espacio entre los conductores