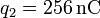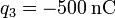Cuatro cargas en un rectángulo

De Laplace

(Diferencias entre revisiones)

Revisión de 16:48 8 ene 2010

1 Enunciado

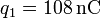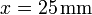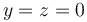Una carga puntual $q_1 = 108\,\mathrm{nC}$ se encuentra situada en el origen de coordenadas. En $x=25\,\mathrm{mm}$ , $y=z=0\,$ se halla una segunda carga $q 2$ . En 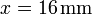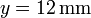$x=16\,\mathrm{mm}$ , $y=12\,\mathrm{mm}$ se encuentra una tercera carga $q 3$ .

Calcule el valor que deben tener $q 2$ y $q 3$ si, ocupando las posiciones indicadas, se desea que sea nula la fuerza sobre una carga 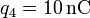$q_4=10\,\mathrm{nC}$ situada en 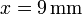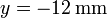$x=9\,\mathrm{mm}$ , $y=-12\,\mathrm{mm}$ , $z = 0$ .

2 Solución

La fuerza sobre la carga $q 4$ es, de acuerdo con la ley de Coulomb y el principio de superposición

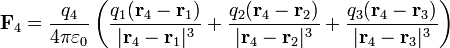
$\mathbf{F}_4 = \frac{q_4}{4\pi\varepsilon_0}\left(\frac{q_1(\mathbf{r}_4-\mathbf{r}_1)}{|\mathbf{r}_4-\mathbf{r}_1|^3}+\frac{q_2(\mathbf{r}_4-\mathbf{r}_2)}{|\mathbf{r}_4-\mathbf{r}_2|^3}+\frac{q_3(\mathbf{r}_4-\mathbf{r}_3)}{|\mathbf{r}_4-\mathbf{r}_3|^3}\right)$

En nuestro caso, midiendo las distancias en milímetros, tenemos que

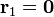
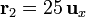
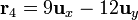
$\mathbf{r}_1=\mathbf{0}\,$ $\mathbf{r}_2=25\,\mathbf{u}_x$ $\mathbf{r}_3=16\mathbf{u}_x+12\mathbf{u}_y\,$ $\mathbf{r}_4=9\mathbf{u}_x-12\mathbf{u}_y$

La posición relativa de $q 4$ respecto a las otras tres cargas y las distancias correspondientes son

De $q 4$ a $q 1$

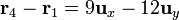
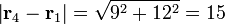
$\mathbf{r}_4-\mathbf{r}_1 = 9\mathbf{u}_x-12\mathbf{u}_y$ $\Rightarrow$ $\left|\mathbf{r}_4-\mathbf{r}_1\right| = \sqrt{9^2+12^2}=15$

De $q 4$ a $q 2$

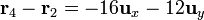
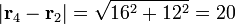
$\mathbf{r}_4-\mathbf{r}_2 = -16\mathbf{u}_x-12\mathbf{u}_y$ $\Rightarrow$ $\left|\mathbf{r}_4-\mathbf{r}_2\right| = \sqrt{16^2+12^2}=20$

De $q 4$ a $q 3$

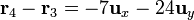
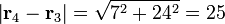
$\mathbf{r}_4-\mathbf{r}_3 = -7\mathbf{u}_x-24\mathbf{u}_y$ $\Rightarrow$ $\left|\mathbf{r}_4-\mathbf{r}_3\right| = \sqrt{7^2+24^2}=25$

Por tanto, la fuerza sobre $q 4$ es, midiendo las cargas en nanoculombios y las distancias en milímetros,

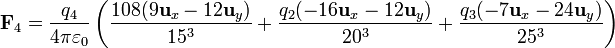
$\mathbf{F}_4=\frac{q_4}{4\pi\varepsilon_0}\left(\frac{108(9\mathbf{u}_x-12\mathbf{u}_y)}{15^3}+\frac{q_2(-16\mathbf{u}_x-12\mathbf{u}_y)}{20^3}+\frac{q_3(-7\mathbf{u}_x-24\mathbf{u}_y)}{25^3}\right)$

Para que esta fuerza sea nula debe serlo cada una de sus componentes, lo que nos da las ecuaciones

$0=\frac{36}{25}-\frac{q_2}{500}-\frac{7q_3}{15625}$ $0=-\frac{48}{125}-\frac{3q_2}{2000}-\frac{24q_3}{15625}$

cuya solución es

$q_2= 256\,\mathrm{nC}$ $q_3=-500\,\mathrm{nC}$

@@ Línea 31: / Línea 31: @@
 Para que esta fuerza sea nula debe serlo cada una de sus componentes, lo que nos da las ecuaciones
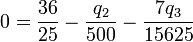
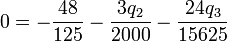
-<center><center><math>0=\frac{36}{25}-\frac{q_2}{500}-\frac{7q_3}{15625}</math></center>{{qquad}}{{qquad}}<math>0=-\frac{48}{125}-\frac{3q_2}{2000}-\frac{24q_3}{15625}</math></center>
+<center><math>0=\frac{36}{25}-\frac{q_2}{500}-\frac{7q_3}{15625}</math>{{qquad}}{{qquad}}<math>0=-\frac{48}{125}-\frac{3q_2}{2000}-\frac{24q_3}{15625}</math></center>
 cuya solución es

Cuatro cargas en un rectángulo

De Laplace

Revisión de 16:48 8 ene 2010

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES