Problemas de Inducción electromagnética
De Laplace
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
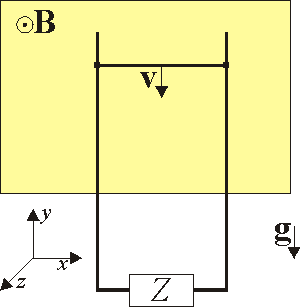
| - | #[[Image:barraquecae.gif|right]] La figura representa un carril metálico superconductor por el cual puede deslizarse una varilla horizontal, también superconductora. Esta varilla está inmersa en un campo uniforme <math>\mathbf{B}_0</math> y cae por la acción de la gravedad | + | #[[Image:barraquecae.gif|right]] La figura representa un carril metálico superconductor por el cual puede deslizarse una varilla horizontal, también superconductora. Esta varilla está inmersa en un campo uniforme <math>\mathbf{B}_0</math> y cae por la acción de la gravedad. <br> |
| - | + | Inicialmente se encuentra en reposo y no circula intensidad por el circuito. En este momento se suelta. Determine la ecuación de movimiento y la posición de la varilla en función del tiempo si el circuito está cerrado por: | |
| - | + | ## Una resistencia <math>R\,</math> | |
| - | + | ## Un condensador <math>C\,</math> | |
| - | # Una resistencia <math>R\,</math> | + | ## Una autoinducción <math>L\,</math>. |
| - | # Un condensador <math>C\,</math> | + | Estudie en cada caso el balance energético del sistema. |
| - | # Una autoinducción <math>L\,</math>. | + | |
| - | + | ||
| - | + | ||
Revisión de 12:13 21 may 2008
- La figura representa un carril metálico superconductor por el cual puede deslizarse una varilla horizontal, también superconductora. Esta varilla está inmersa en un campo uniforme
 y cae por la acción de la gravedad.
y cae por la acción de la gravedad.
Inicialmente se encuentra en reposo y no circula intensidad por el circuito. En este momento se suelta. Determine la ecuación de movimiento y la posición de la varilla en función del tiempo si el circuito está cerrado por:
- Una resistencia

- Un condensador

- Una autoinducción
 .
.
- Una resistencia
Estudie en cada caso el balance energético del sistema.