Integral sobre una superficie esférica
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 35: | Línea 35: | ||
parecería que la integral vale | parecería que la integral vale | ||
| - | <center><math>\mathbf{I}=-4\pi R^2\mathbf{u}_{\theta}</math>{{qquad}}<span style="background:red;color:white">RESULTADO INCORRECTO</span></center> | + | <center><math>\mathbf{I}=-4\pi R^2\mathbf{u}_{\theta}(\theta,\varphi)</math>{{qquad}}<span style="background:red;color:white">RESULTADO INCORRECTO</span></center> |
Este resultado es incorrecto porque no se ha tenido en cuenta que <math>\mathbf{u}_{r}</math> y <math>\mathbf{u}_{\theta}</math> dependen de la posición y, por tanto, también deben ser integrados. Se llega además al resultado absurdo de que el valor final de la integral va en la dirección de <math>\mathbf{u}_{\theta}(\theta,\varphi)</math>; es decir, ¡es distinto en cada punto de la esfera!, lo cual es absurdo ya que se trata de una integral definida. | Este resultado es incorrecto porque no se ha tenido en cuenta que <math>\mathbf{u}_{r}</math> y <math>\mathbf{u}_{\theta}</math> dependen de la posición y, por tanto, también deben ser integrados. Se llega además al resultado absurdo de que el valor final de la integral va en la dirección de <math>\mathbf{u}_{\theta}(\theta,\varphi)</math>; es decir, ¡es distinto en cada punto de la esfera!, lo cual es absurdo ya que se trata de una integral definida. | ||
| Línea 43: | Línea 43: | ||
En nuestro caso, debemos aplicar que | En nuestro caso, debemos aplicar que | ||
| - | <center><math>\mathbf{u}_{r}=\mathrm{sen}\,\theta\,\cos\varphi\,\mathbf{u}_{x}+\mathrm{sen}\,\theta\,\mathrm{sen}\varphi\,\mathbf{u}_{y}+\cos\theta\,\mathbf{u}_{z}</math>{{qquad}} | + | <center><math>\mathbf{u}_{r}(\theta,\varphi)=\mathrm{sen}\,\theta\,\cos\varphi\,\mathbf{u}_{x}+\mathrm{sen}\,\theta\,\mathrm{sen}\varphi\,\mathbf{u}_{y}+\cos\theta\,\mathbf{u}_{z}</math>{{qquad}} |
| - | <math>\mathbf{u}_{\theta}=\cos\theta\,\cos\varphi\,\mathbf{u}_{x}+\cos\theta\,\mathrm{sen}\varphi\,\mathbf{u}_{y}-\mathrm{sen}\,\theta\,\mathbf{u}_{z}</math></center> | + | <math>\mathbf{u}_{\theta}(\theta,\varphi)=\cos\theta\,\cos\varphi\,\mathbf{u}_{x}+\cos\theta\,\mathrm{sen}\varphi\,\mathbf{u}_{y}-\mathrm{sen}\,\theta\,\mathbf{u}_{z}</math></center> |
de forma que | de forma que | ||
Revisión de 06:34 5 oct 2009
1 Enunciado
Halle el valor de la integral
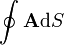
con
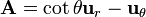
y la superficie de integración una esfera de radio R centrada en el origen.
2 Solución
Este problema ilustra algunos errores comunes a la hora de calcular integrales empleando coordenadas curvilíneas.
Un primer impulso sería el de aplicar el teorema de Gauss y convertir la integral en una de volumen. Sin embargo, esta integral no es un flujo, sino una vectorial; dS es el área de un elemento, no el vector diferencial de superficie. Por ello, el teorema no se puede aplicar de forma inmediata.
El segundo error frecuente, al calcular la integral de superficie, consiste en olvidar que los propios vectores de la base son funciones de la posición.
Comenzamos observando que, por tratarse de la superficie de una esfera, el diferencial de superficie es

con lo que la integral puede escribirse

Si se aplica que el integrando no depende de  y que
y que

parecería que la integral vale
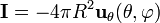 RESULTADO INCORRECTO
RESULTADO INCORRECTOEste resultado es incorrecto porque no se ha tenido en cuenta que 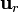 y
y 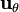 dependen de la posición y, por tanto, también deben ser integrados. Se llega además al resultado absurdo de que el valor final de la integral va en la dirección de
dependen de la posición y, por tanto, también deben ser integrados. Se llega además al resultado absurdo de que el valor final de la integral va en la dirección de  ; es decir, ¡es distinto en cada punto de la esfera!, lo cual es absurdo ya que se trata de una integral definida.
; es decir, ¡es distinto en cada punto de la esfera!, lo cual es absurdo ya que se trata de una integral definida.
Para realizar correctamente esta integral deben usarse vectores expresados en la base cartesiana, que es la única que no depende de la posición y puede salir de la integral. Ello no impide el uso de las coordenadas curvilíneas para expresar los vectores.
En nuestro caso, debemos aplicar que
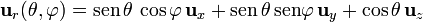
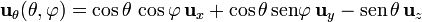
de forma que
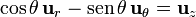
Obsérvese que este vector tiene igual módulo dirección y sentido en todos los puntos de la esfera, por lo que puede salir de la integral, pues no depende de las variables de integración. Se obtiene así el resultado correcto de la integral,
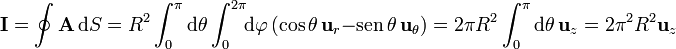
resultado que sí tiene sentido, pues 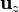 es un vector perfectamente definido para la esfera.
es un vector perfectamente definido para la esfera.





