Masa que cuelga de dos muelles
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Se tiene una masa <math>m</math> que cuelga de una asociación de dos muelles en paralelo con constantes recuperadoras <math>k_1</math> y <math>k_2</math> y longitudes ...) |
|||
| Línea 11: | Línea 11: | ||
==Elongación de equilibrio== | ==Elongación de equilibrio== | ||
| + | La condición de equilibrio para la masa es | ||
| + | |||
| + | <center><math>\sum_i \mathbf{F}_i=\mathbf{0}</math></center> | ||
| + | |||
| + | donde las fuerzas que actúan sobre la masa son las dos fuerzas elásticas y el peso. Tomando, como se indica, el eje Y vertical y hacia abajo, las fuerzas valen | ||
| + | |||
| + | <center><math>\mathbf{F}_1 = -k_1(L_\mathrm{eq}-L_1)\mathbf{j}\,</math>{{qquad}}{{qquad}}<math>\mathbf{F}_2 = -k_2(L_\mathrm{eq}-L_2)\mathbf{j}\,</math>{{qquad}}{{qquad}}<math>\mathbf{F}_3=\mathbf{P}=mg\mathbf{j}\,</math></center> | ||
| + | |||
| + | Sumando e igualando a cero | ||
| + | |||
| + | <center><math>-k_1(L_\mathrm{eq}-L_1)-k_2(L_\mathrm{eq}-L_2) + mg = 0\,</math></center> | ||
| + | |||
| + | y despejando | ||
| + | |||
| + | <center><math>L_\mathrm{eq}=\frac{mg+k_1L_1+k_2L_2}{k_1+k_2}</math></center> | ||
| + | |||
| + | Vemos que la posición de equilibrio '''no''' es igual al peso dividida por la constante de la asociación, ya que hay que tener en cuenta la diferencia en las longitudes naturales. | ||
==Propiedades de la oscilación== | ==Propiedades de la oscilación== | ||
==Onda sonora== | ==Onda sonora== | ||
==Valores numéricos== | ==Valores numéricos== | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 14:52 19 jun 2009
Contenido |
1 Enunciado
Se tiene una masa m que cuelga de una asociación de dos muelles en paralelo con constantes recuperadoras k1 y k2 y longitudes naturales L1 y L2, respectivamente.
- Determine el valor de la elongación de la asociación en la situación de equilibrio.
- Se empuja la masa verticalmente hacia arriba con una velocidad inicial v0. Suponiendo que el rozamiento es despreciable, encuentre la evolución de la posición de la masa en el tiempo y el período de oscilación (Escoja como origen de coordenadas la posición de equilibrio del apartado anterior). Calcule la posición más alta que alcanza la masa y su energía en ese instante.
- Se añade un pistón de masa despreciable, de modo que se mueve dentro de un cilindro relleno con nitrógeno. Determine la longitud de onda de la onda de sonido generada en el cilindro, considerando que el gas es ideal.
- Determine los valores numÚricos de las magnitudes pedidas en los apartados anteriores.
Datos: 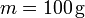 ,
, 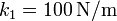 ,
, 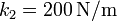 ,
,
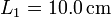 ,
, 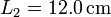 ,
, 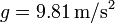 ,
, 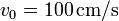 ,
, 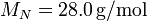 ,
, 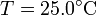
2 Elongación de equilibrio
La condición de equilibrio para la masa es
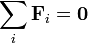
donde las fuerzas que actúan sobre la masa son las dos fuerzas elásticas y el peso. Tomando, como se indica, el eje Y vertical y hacia abajo, las fuerzas valen

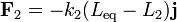

Sumando e igualando a cero
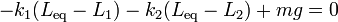
y despejando
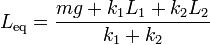
Vemos que la posición de equilibrio no es igual al peso dividida por la constante de la asociación, ya que hay que tener en cuenta la diferencia en las longitudes naturales.





