Fuerza entre conductores con dieléctricos entre ellos
De Laplace
(Diferencias entre revisiones)
(→Planteamiento) |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | [[Imagen:esferas2dielectricos.png|right]]En un sistema formado por dos esferas metálicas concéntricas de radios <math>a</math> y <math>c</math>, entre las cuales se encuentran dos medios dieléctricos, con una interfaz ecuatorial, | + | [[Imagen:esferas2dielectricos.png|right]]En un sistema formado por dos esferas metálicas concéntricas de radios <math>a</math> y <math>c</math>, entre las cuales se encuentran dos medios dieléctricos, con una interfaz ecuatorial. Cuando el conductor interior almacena una carga <math>Q</math>, aparece una fuerza de atracción entre los electrodos, que está ausente si solo hay un medio dieléctrico que llene todo el espacio entre las placas. Se trata de calcular esta fuerza. |
# Determine la densidad de carga libre en la superficie del electrodo interior. | # Determine la densidad de carga libre en la superficie del electrodo interior. | ||
Revisión de 20:03 8 jun 2009
Contenido |
1 Enunciado
- Determine la densidad de carga libre en la superficie del electrodo interior.
- Halle el valor del campo eléctrico en los mismos puntos.
- La fuerza sobre un elemento de superficie conductora es
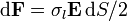. Integrando esta fuerza elemental, determine la fuerza neta sobre el electrodo interior. ¿Hacia donde va dirigida? ¿Cuál es el origen de esta fuerza?
- De forma análoga, calcule la fuerza sobre el electrodo exterior. ¿Se verifica la tercera ley de Newton?
2 Introducción
3 Densidad de carga libre
3.1 Planteamiento
Para determinar la densidad de carga libre debemos calcular previamente el vector desplazamiento, cuya discontinuidad nos da la densidad de carga. A su vez, para hallar el vector 
debemos determinar simultáneamente el campo eléctrico.
Alternativamente podemos hallar en primer lugar la distribución de potencial eléctrico, y a partir de éste el campo, el desplazamiento y la carga libre. No obstante, dada la simplicidad de las ecuaciones que aparecen en este problema, no es necesario recurrir al potencial y pude resolverse completamente empleando solo 
}y
