Ejemplos de superficies equiescalares
De Laplace
(→Enlaces) |
(→Enlaces) |
||
| Línea 88: | Línea 88: | ||
* '''Anterior:''' [[Superficies equiescalares]] | * '''Anterior:''' [[Superficies equiescalares]] | ||
| - | [[Categoría: | + | [[Categoría:Campos escalares y vectoriales|40]] |
Revisión de 18:14 2 dic 2007
Contenido |
1 Superficies de fase constante
En el estudio de la ondas electromagnéticas aparecen frecuentemente las superficies de fase constante, que son las equiescalares de la fase de oscilación de la onda en cada punto. En el caso particular de las ondas planas, estas superficies verifican
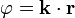
donde 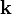 es un vector constante (el vector de onda) y
es un vector constante (el vector de onda) y 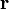 es el vector de posición. Para describir las superficies equipotenciales podemos suponer que
es el vector de posición. Para describir las superficies equipotenciales podemos suponer que 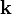 tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué.
tiene componentes según los tres ejes de coordenadas, pero en realidad no tenemos por qué.
Puesto que los ejes no están fijados de antemano, podemos elegirlos como más nos convenga. En particular, podemos tomar el eje  apuntando en la dirección de
apuntando en la dirección de 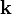 , de forma que este vector se escribe
, de forma que este vector se escribe

y el campo escalar 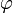 es simplemente
es simplemente
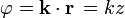
por tanto las superficies equiescalares son planos paralelos entre sí
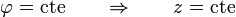
Estos planos son perpendiculares al eje  . Por tanto, las superficies de fase constante de
. Por tanto, las superficies de fase constante de 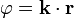 son planos paralelos entre sí y perpendiculares al vector
son planos paralelos entre sí y perpendiculares al vector 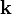 .
.
2 Un campo inversamente proporcional a la distancia
En el estudio del potencial eléctrico de cargas puntuales, aparece el campo escalar
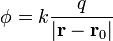
donde 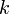 y
y 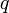 son constantes,
son constantes, 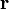 es el vector de posición (variable) y
es el vector de posición (variable) y 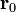 un punto fijo. Las superficies equiescalares verifican
un punto fijo. Las superficies equiescalares verifican

Por definición, el lugar geométrico de los puntos que equidistan de un punto fijo forman una superficie esférica. El centro será el punto 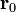 y el radio
y el radio 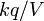 .
.
Puesto que el centro es el mismo para todas las esferas, mientras que el radio depende del valor del potencial, resulta que las superficies equiescalares constituyen una familia de esferas concéntricas.
3 Simetría traslacional
Supongamos un campo escalar de la forma

con  una constante. Examinando la forma funcional de este campo, vemos que no depende de la coordenada
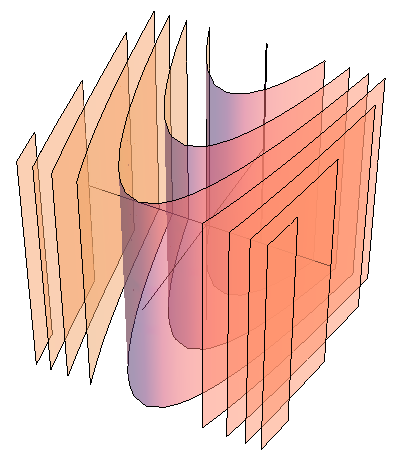
una constante. Examinando la forma funcional de este campo, vemos que no depende de la coordenada  , esto es, posee simetría traslacional. Lo que esto implica para sus superficies equiescalares es que estas son cilíndricas, lo cual no quiere decir que tengan forma de cilindros circulares, sino que se extienden paralelamente al eje
, esto es, posee simetría traslacional. Lo que esto implica para sus superficies equiescalares es que estas son cilíndricas, lo cual no quiere decir que tengan forma de cilindros circulares, sino que se extienden paralelamente al eje  .
.
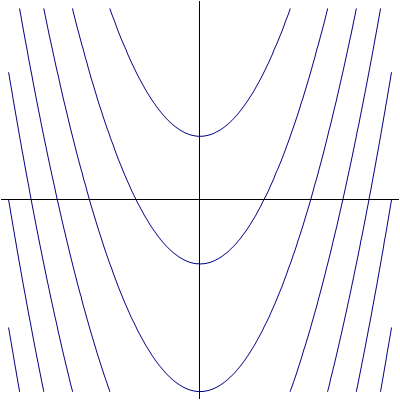
El corte de estas superficies con el plano  nos da las bases de las superficies cilíndricas. En este caso
nos da las bases de las superficies cilíndricas. En este caso
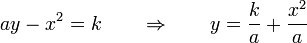
En el plano  resultan parábolas. Por tanto las superficies equiescalares son cilindros parabólicos (que no paraboloides, que eso es otra cosa).
resultan parábolas. Por tanto las superficies equiescalares son cilindros parabólicos (que no paraboloides, que eso es otra cosa).
3.1 ¿Por qué la  ?
?
Puede parecer raro, especielmente si uno acude a lo que se estudia en asignaturas de matemáticas, que a la hora de escribir el campo sea necesario poner 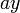 y no simplemente
y no simplemente  . La razón es que, en física, las magnitudes tienen dimensiones, y no pueden sumarse peras con manzanas. Una superficie, como
. La razón es que, en física, las magnitudes tienen dimensiones, y no pueden sumarse peras con manzanas. Una superficie, como 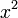 no puede sumarse con una distancia,
no puede sumarse con una distancia, 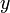 . Para poder efectuar la suma es necesario incluir una constante
. Para poder efectuar la suma es necesario incluir una constante  con dimensiones de distancia.
con dimensiones de distancia.
4 Simetría acimutal
Consideremos ahora el campo
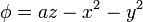
Este campo no posee simetría traslacional, pero si acimutal. Para verlo lo escribimos en coordenadas cilíndricas, como
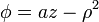
que es independiente de la coordenada  .
.
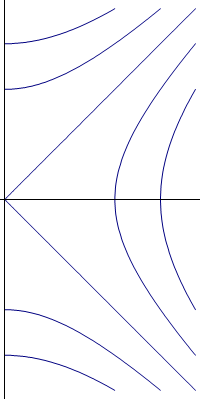
Para las equipotenciales esta simetría implica que son superficies de revolución, esto es, que se obtienen al girar curvas del semiplano 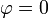 (
(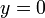 , con
, con 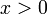 ) alrededor del eje
) alrededor del eje  .
.
En nuestro caso particular, las curvas son hipérbolas (o arcos de hipérbola, pues son media hipérbola) y las superficies equipotenciales son hiperboloides
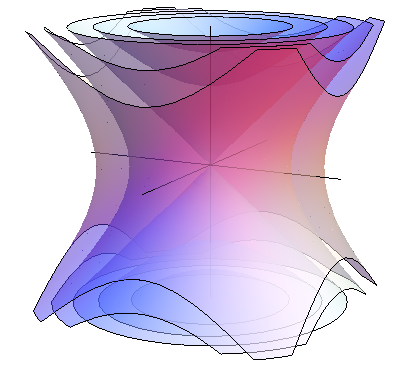
5 Un ejemplo aparentemente más complicado
Supongamos que se nos pide dibujar las superficies equiescalares del campo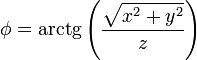
Aunque de entrada puede parecer complicado, si recordamos las relaciones entre los distintos sistemas de coordenadas podemos ver que
y por tanto las superficies 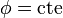 son conos rectos con vértice el origen y eje el eje
son conos rectos con vértice el origen y eje el eje  .
.
Estas superficies también poseen simetría acimutal.
6 Enlaces
- Siguiente: Representación de campos vectoriales
- Anterior: Superficies equiescalares






