Material magnético lineal
De Laplace
(Nueva página: ==Definición== {{ac|Material magnético lineal}} Son aquellos en los que la magnetización es proporcional al campo magnético <math>\mathbf{H}</math> <center><math>\mathbf{M} = \ch...) |
(→Definición) |
||
| Línea 1: | Línea 1: | ||
==Definición== | ==Definición== | ||
| - | |||
Son aquellos en los que la magnetización es proporcional al campo magnético <math>\mathbf{H}</math> | Son aquellos en los que la magnetización es proporcional al campo magnético <math>\mathbf{H}</math> | ||
Revisión de 12:06 10 abr 2009
1 Definición
Son aquellos en los que la magnetización es proporcional al campo magnético 
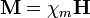
siendo χm la susceptibilidad magnética. Para los medios lineales, el campo magnético 
es también proporcional al campo magnético
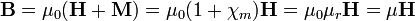
La cantidad μr = 1 + χm es la denominada permeabilidad relativa del medio, mientras que μ = μ0μr es la permeabilidad absoluta.
Dependiendo del signo de χm, los materiales lineales se dividen en dos grupos: diamagnéticos y paramagnéticos.
1.1 Diamagnéticos
Poseen una susceptibilidad negativa. En estos materiales, el campo se ve reducido por efecto de la magnetización inducida, que se opone al campo externo. Para casi todos los diamagnéticos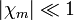 
y puede aproximarse 
.
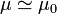1.2 Paramagnéticos
Tienen una susceptibilidad positiva. En los materiales paramagnéticos la magnetización refuerza al campo externo. La mayoría de los medios paramagnéticos tienen una susceptibilidad muy pequeña y 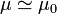. No obstante, existen sustancias paramagnéticas con muy alta susceptibilidad; estas sustancias, a bajas temperaturas se transforman en ferromagnéticas.
