Imán cilíndrico

De Laplace

Revisión de 12:49 31 mar 2009

1 Enunciado

Se construye un imán cilíndrico de radio R = 1cm y longitud L, con una magnetización uniforme y paralela a su eje M₀ = 10⁵A / m.

1. Determine aproximadamente los campos y cuando 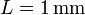, en el centro del imán y en un punto ligeramente por encima de su base superior.
   1. A partir de las corrientes de magnetización.
   2. A partir de las cargas magnéticas.
2. Estime y cuando 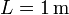en los mismos puntos y con los mismos métodos
3. Determine exactamente y en todos los puntos del eje del imán, tanto dentro como fuera de él. Compare con los resultados anteriores

2 Imán corto

Cuando el imán se reduce a un disco, porque 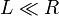, como ocurre en este caso (R = 1 cm, L = 1 mm), podemos calcular el campo de dos formas: empleando las corrientes de magnetización, o empleando las cargas magnéticas

2.1 Empleando las corrientes

Por ser la imanación 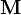uniforme, no hay corrientes de volumen, pero sí superficiales. Puesto que la magnetización es perpendicular a las bases del disco, las únicas corrientes de imanación están en la cara lateral y valen

Así pues, el disco imanado es aproximadamente equivalente a una espira de corriente por la que circula una intensidad

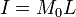
2.1.1 En el centro del imán

A partir de esta equivalencia, es inmediato conocer el campo en el centro del imán, pues el campo de una espira circular es un problema clásico con solución

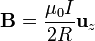
y en nuestro caso resulta un campo

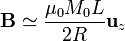
Una vez conocido el valor de , el cálculo de es inmediato

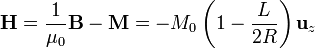
Nótese que, de los dos términos del paréntesis, el segundo representa una corrección al primero, pues .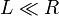

Los valores numéricos de estos dos campos en esta aproximación son (en el Sistema Internacional)

        

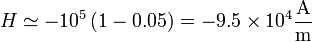
2.1.2 Justo encima del imán

Para un punto ligeramente por encima del disco, el campo es el mismo pues la espira equivalente se puede considerar prácticamente como plana, pero el campo cambia pues en el exterior del imán la magnetización es nula (el vacío no se magnetiza). Esto da

        

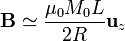
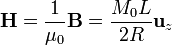
2.2 Empleando las cargas

Este mismo sistema puede modelarse considerando densidades de carga magnética equivalentes. De nuevo, por ser la magnetización uniforme, no hay densidad volumétrica, pero sí superficial, dada por la expresión

En este caso, 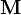es tangente a la cara lateral y sobre la misma no hay densidades de carga, pero sí sobre las bases. Sobre la cara superior será

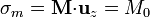
y, sobre la inferior

esto es, el imán es equivalente a dos discos de carga de signos opuestos y muy próximos entre sí. Esto es el análogo magnético de lo que en electrostática es un condensador.

Sabemos que el campo eléctrico en un condensador de placas planas y paralelas, despreciando los efectos de borde, con densidad de carga σ_s en la cara positiva, es

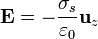
En nuestro caso, las ecuaciones para son las mismas que para , salvo que no aparece . Esto nos da para el campo

y, a partir de , se obtiene

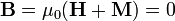
El valor numérico es inmediato

        

Vemos que, en esta aproximación resulta un campo magnético nulo en el interior, mientras que antes resultaba un valor distinto de cero. Si comparamos las dos expresiones vemos que en este caso se ha despreciado la primera corrección, proporcional a L / R que allí sí aparecía.

En cuanto a un punto en el exterior, sabemos que fuera de un condensador el campo es nulo (aproximadamente), por lo que

        

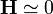
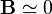
3 Imán largo

Cuando el imán es muy largo, podemos, de nuevo, obtener soluciones aproximadas por los dos modelos

3.1 Empleando las corrientes

3.2 Empleando las cargas

4 Imán de longitud arbitraria