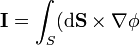Generalización del teorema de Stokes
De Laplace
(→Teorema de Stokes) |
(→Generalización a un campo escalar) |
||
| Línea 7: | Línea 7: | ||
==Generalización a un campo escalar== | ==Generalización a un campo escalar== | ||
| + | La primera generalización viene de considerar la integral vectorial | ||
| + | |||
| + | <center><math>\mathbf{I}=\oint_\Gamma \mathrm{d}\mathbf{r}\,\phi</math></center> | ||
| + | |||
| + | Esta integral no es una circulación, sino que da como resultado un vector, obtenido sumando el valor del campo escalar <math>\phi</math> en cada punto de <math>\Gamma</math> multiplicado por el desplazamiento diferencial a lo largo de la curva. | ||
| + | |||
| + | La pregunta que nos hacemos es si podemos convertir esta integral en una sobre la superficie <math>S</math> apoyada en <math>\Gamma</math>. Para ver cómo, multiplicamos la integral por un vector constante <math>\mathbf{u}</math> | ||
| + | |||
| + | <center><math>\mathbf{u}\cdot\mathbf{I}=\mathbf{u}\cdot\oint_\Gamma \mathrm{d}\mathbf{r}\,\phi=\oint_\Gamma \mathrm{d}\mathbf{r}\cdot\mathbf{u}\phi</math></center> | ||
| + | |||
| + | El vector puede entrar en la integral por ser constante. Ahora sí tenemos una circulación, a la que se puede aplicar el teorema de Stokes | ||
| + | |||
| + | <center><math>\mathbf{u}\cdot\mathbf{I}=\oint_\Gamma \mathrm{d}\mathbf{r}\cdot(\mathbf{u}\phi)=\int_S\mathrm{d}\mathbf{S}\cdot\nabla\times(\mathbf{u}\phi)</math></center> | ||
| + | |||
| + | Desarrollando el rotacional del producto de un escalar por un vector | ||
| + | |||
| + | <center><math>\nabla\times(\mathbf{u}\phi)=\overbrace{\nabla\times\mathbf{u}}^{=0}\phi+(\nabla\phi)\times\mathbf{u} = (\nabla\phi)\times\mathbf{u}</math></center> | ||
| + | |||
| + | Sustituyendo en la expresión anterior | ||
| + | |||
| + | <center><math>\mathbf{u}\cdot\mathbf{I}=\int_S\mathrm{d}\mathbf{S}\cdot(\nabla\phi\times\mathbf{u})</math></center> | ||
| + | |||
| + | Aplicando ahora la propiedad del producto mixto | ||
| + | |||
| + | <center><math>\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})=(\mathbf{A}\times\mathbf{B})\cdot\mathbf{C}</math></center> | ||
| + | |||
| + | nos queda | ||
| + | |||
| + | <center><math>\mathbf{u}\cdot\mathbf{I}=\int_S(\mathrm{d}\mathbf{S}\times\nabla\phi)\cdot\mathbf{u}</math></center> | ||
| + | |||
| + | Aplicando de nuevo que <math>\mathbf{u}</math> es un vector constante | ||
| + | |||
| + | <center><math>\mathbf{u}\cdot\mathbf{I}=\mathbf{u}\cdot\left(\int_S(\mathrm{d}\mathbf{S}\times\nabla\phi\right)</math></center> | ||
| + | |||
| + | y, puesto que esta identidas se verifica sea cual sea el vector <math>\mathbf{u}</math>, debe cumplirse que | ||
| + | |||
| + | <center><math>\mathbf{I}=\int_S(\mathrm{d}\mathbf{S}\times\nabla\phi</math></center> | ||
==Generalización a un producto vectorial== | ==Generalización a un producto vectorial== | ||
Revisión de 18:37 26 mar 2009
Contenido |
1 Teorema de Stokes
El teorema de Stokes establece que, dada una curva cerrada Γ, la circulación de un campo vectorial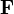 
equivale al flujo de su rotacional a través de una superficie S arbitraria con Γ como borde, y orientada según la regla de la mano derecha
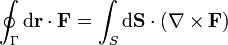
Este teorema es sólo uno de una familia de teoremas de estructura similar.
2 Generalización a un campo escalar
La primera generalización viene de considerar la integral vectorial
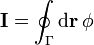
Esta integral no es una circulación, sino que da como resultado un vector, obtenido sumando el valor del campo escalar φ en cada punto de Γ multiplicado por el desplazamiento diferencial a lo largo de la curva.
La pregunta que nos hacemos es si podemos convertir esta integral en una sobre la superficie S apoyada en Γ. Para ver cómo, multiplicamos la integral por un vector constante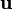 
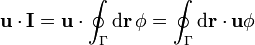
El vector puede entrar en la integral por ser constante. Ahora sí tenemos una circulación, a la que se puede aplicar el teorema de Stokes
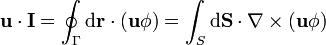
Desarrollando el rotacional del producto de un escalar por un vector
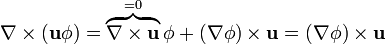
Sustituyendo en la expresión anterior
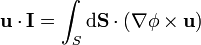
Aplicando ahora la propiedad del producto mixto
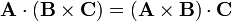
nos queda
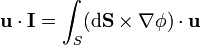
Aplicando de nuevo que 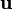es un vector constante
y, puesto que esta identidas se verifica sea cual sea el vector 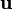, debe cumplirse que
