Generalización del teorema de Stokes
De Laplace
(Diferencias entre revisiones)
(→Teorema de Stokes) |
(→Teorema de Stokes) |
||
| Línea 3: | Línea 3: | ||
<center><math>\oint_\Gamma \mathrm{d}\mathbf{r}\cdot\mathbf{F} = \int_S \mathrm{d}\mathbf{S}\cdot(\nabla\times\mathbf{F})</math></center> | <center><math>\oint_\Gamma \mathrm{d}\mathbf{r}\cdot\mathbf{F} = \int_S \mathrm{d}\mathbf{S}\cdot(\nabla\times\mathbf{F})</math></center> | ||
| + | |||
| + | Este teorema es sólo uno de una familia de teoremas de estructura similar. | ||
==Generalización a un campo escalar== | ==Generalización a un campo escalar== | ||
Revisión de 17:26 26 mar 2009
Contenido |
1 Teorema de Stokes
El teorema de Stokes establece que, dada una curva cerrada Γ, la circulación de un campo vectorial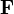 
equivale al flujo de su rotacional a través de una superficie S arbitraria con Γ como borde, y orientada según la regla de la mano derecha
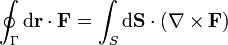
Este teorema es sólo uno de una familia de teoremas de estructura similar.
