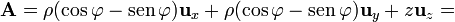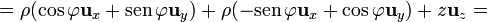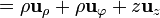Integrales de camino. Ejemplos
De Laplace
(→Elección del sistema de coordenadas) |
(→Elección del sistema de coordenadas) |
||
| Línea 20: | Línea 20: | ||
<center><math>\mathbf{A} = \rho(\cos\varphi-\mathrm{sen}\,\varphi)\mathbf{u}_{x}+\rho(\cos\varphi-\mathrm{sen}\,\varphi)\mathbf{u}_y+z\mathbf{u}_{z} =</math> | <center><math>\mathbf{A} = \rho(\cos\varphi-\mathrm{sen}\,\varphi)\mathbf{u}_{x}+\rho(\cos\varphi-\mathrm{sen}\,\varphi)\mathbf{u}_y+z\mathbf{u}_{z} =</math> | ||
| - | |||
<math>= \rho(\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\varphi\mathbf{u}_y)+\rho(-\mathrm{sen}\,\varphi\mathbf{u}_x+\cos\varphi\mathbf{u}_y)+z\mathbf{u}_{z} =</math> | <math>= \rho(\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\varphi\mathbf{u}_y)+\rho(-\mathrm{sen}\,\varphi\mathbf{u}_x+\cos\varphi\mathbf{u}_y)+z\mathbf{u}_{z} =</math> | ||
| - | |||
<math>=\rho\mathbf{u}_\rho +\rho\mathbf{u}_\varphi + z\mathbf{u}_{z}</math></center> | <math>=\rho\mathbf{u}_\rho +\rho\mathbf{u}_\varphi + z\mathbf{u}_{z}</math></center> | ||
Revisión de 13:46 23 nov 2007
Contenido |
1 Un ejemplo sencillo
1.1 Enunciado
Por poner un ejemplo de integral de camino, supongamos que nos piden, dado el campo
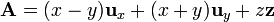
hallar la integral
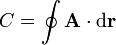
sobre una circunferencia de radio 
situada en el plano 
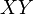y con centro el origen de coordenadas (el circulito de la integral significa que la integral se hace sobre una curva cerrada).
1.2 Elección del sistema de coordenadas
El camino de integración es una circunferencia horizontal, lo que corresponde a una línea coordenada de la coordenada 
.
Por ello, parece conveniente elegir o bien coordenadas cilíndricas o bien coordenadas esféricas (ya que ambos sistemas comparten la coordenada ). Como el sistema cilíndrico parece más sencillo que el esférico, nos quedaremos con él.
El problema es que el vector que hay que integrar viene expresado en cartesianas, así que hay que pasarlo a cilíndricas. Si sustituimos las expresiones de las coordenadas
